最近学习了条件随机场CRF,做下总结。主要参考BiLSTM+CRF模型中的CRF层为主线,结合李航老师的《统计机器学习》,记录自己对CRF的理解。
从马尔科夫随机场到线性链条件随机场
概率图模型
概率图模型是用图G = (V,E)来表示概率分布。设有联合概率分布P(Y),Y是一组随机变量。我们可以用无向图G = (V,E)来表示联合概率分布P(Y),节点$v \in V$表示随机变量$Y_v$,边$e \in E$表示随机变量之间的概率依赖关系。概率无向图模型,即马尔科夫随机场
设有联合概率分布P(Y),由无向图G=(V,E)表示。如果概率分布P(Y)满足成对、局部、全局马尔科夫性,那么称 这个联合概率分布p(Y)为概率无向图模型,或马尔科夫随机场(Markov random field)。成对马尔科夫性、局部马尔可夫性、全部马尔科夫性要表达的就是:在无向图中,没有边连接的节点之间没有概率依赖关系,也就是没有边连接的节点代表的随机变量之间是条件独立的。
条件随机场
设X和Y是随机变量,P(Y|X)是给定X的条件下Y的条件概率分布。若给定X的条件下,Y构成一个马尔科夫随机场。则称条件概率分布P(Y|X)为条件随机场。
我们可以看到,马尔科夫随机场是联合概率分布P(Y),而条件随机场是条件概率分布P(Y|X)。这是一点不同。线性链条件随机场
设$X =(X_1,X_2,…,X_n), Y =(Y_1,Y_2,…,Y_n)$是线性链表示的随机变量序列。若在给定随机变量序列X的条件下,随机变量序列Y的条件概率分布P(Y|X)构成条件随机场,即满足马尔可夫性:$$P(Y_i|X,Y_1,Y_2,…,Y_{i-1},Y_{i+1},…,Y_n) = P(Y_i|X,Y_{i-1},Y_{i+1})$$ 。则称条件概率分布p(Y|X)为线性链条件随机场。
线性链条件随机场和隐马尔可夫模型都是序列模型,可以用于标注问题。这时,条件概率模型P(Y|X)中,X是输入变量序列,表示需要标注的观测序列;Y是输出变量,表示标记序列,或称状态序列。
BiLSTM+CRF模型
BiLSTM+CRF模型是命名实体识别任务的常用模型。
假设我们训练集中有个由五个词组成的句子$X = (w_0,w_1,w_2,w_3,w_4)$,对应标签为$Y = [B-Person,I-Person,O,B-Organization,O]$。数据集中有五类标签:
| 类别 | B-Person | I-Person | B-Organization | I-Organization | O |
|---|---|---|---|---|---|
| 含义 | 人名的开始部分 | 人名的中间部分 | 组织机构的开始部分 | 组织机构的中间部分 | 非实体信息 |
先简单介绍下BiLSTM+CRF模型的结构。LSTM层的输入一般为每个词的Word-embedding,输出为每个词word在类别空间tag_space上的非归一化概率,也就是在单词对应每个类别的得分score。这些score作为CRF层的输入。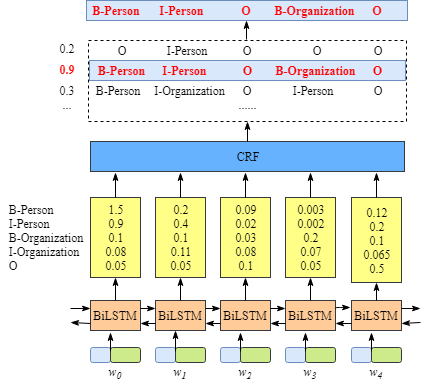
CRF的损失函数
条件随机场中有两个重要的矩阵,转移概率矩阵和状态概率矩阵,分别对应转移特征和状态特征。
- 状态概率矩阵。就是LSTM层的输出,作为CRF层的输入。矩阵的形状为[N,M],N为句子长度,M为可能状态数。
- 转移概率矩阵。矩阵形状为[M,M],M为可能状态数。转移矩阵是模型参数,是随机初始化的,在训练过程中不断更新优化。
给定转移矩阵T,随机变量序列X取值为x的条件下,随机变量序列取值为y的似然函数为:$$Likelihood(y|x,T) = \frac{ \sum_{i=0}^{n} P(x_i|y_i)T(y_i|y_{i-1})}{\sum_{y^}\biggl(\sum_{i=0}^{n}P(x_i|y_i^)T(y_i^|y_{i-1}^)\biggr)} \cdots\cdots\cdots\cdots\cdots (1)$$
上式中,
- $P(x_i|y_i)$表示当前状态为$y_i$时,产生观测值$x_i$的概率。对应状态分数。
- $T(y_i|y_{i-1})$表示从上一个状态$y_{i-1}$转换到当前状态$y_i$的概率。对应转移分数。我们可以从转移矩阵中读出这个概率。
- 分子表示了单条路径y=[y_0,y_1,…,y_n]的分数score或概率。
- 分母表示了所有可能路径$y^*$的总分。注意计算分母时,我们要计算所有可能路径并求和。若序列长度为N,状态可能数为M,则所有可能路径数为$M^N$,这个数量是指数级的,非常大。我们的秘密武器是
前向后向算法来高效地计算分母。
进一步地,负对数似然函数为:
$$NegLogLikelihood(y|x,T) = \sum_{y^}\biggl( \sum_{i=0}^{n} log(P(x_i|y_i^)T(y^_i|y^{i-1}))\biggr) - \sum{i=0}^{n}log(P(x_i|y_i)T(y_i|y_{i-1})) \cdots\cdots\cdots\cdots (2)$$
从式子(1)到式子(2),直接对式子(1)取负对数是得到式子(2)可能比较令人费解。
需要留意的是:转移概率矩阵和状态概率矩阵中的概率都是对数概率(这很重要),这样计算路径概率时都是加法。对对数概率加上exp()运算我们能得到正常概率。
《统计学习方法》书中说,线性链条件随机场是对数线性模型,在对数空间中,对数概率可以直接相加,带来很大的方便。接下来,我们来看看:真实路径的分数和所有路径的总分是怎么计算的?
真实路径分数
数据集中有五类标签,再引入start和end作为序列开始和结束标志。
| 类别 | B-Person | I-Person | B-Organization | I-Organization | O | start | end |
|---|---|---|---|---|---|---|---|
| 索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
长度为5的序列,$X = (w_0,w_1,w_2,w_3,w_4)$,
对应类别为$Y = [B-Person,I-Person,O,B-Organization,O]$,
标注序列,也就是真实路径为为y = [0,1,4,3,4]。
真实路径的分数由两部分组成,状态分数和转移分数。状态矩阵就是LSTM层的输出。转移矩阵是模型参数,为$$[t_{ij}],i,j\in [0,6];i\neq 6,j\neq 5$$其中$t_ij$表示从上一状态转换到当前状态的概率。转移时,不能转移到start,不能从end转移。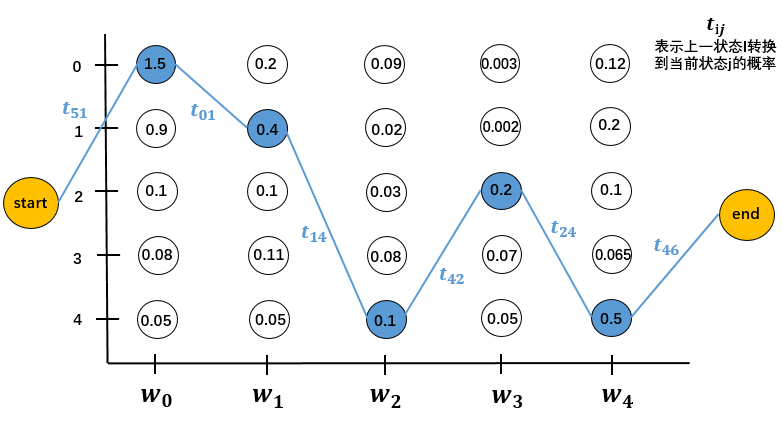
所有路径分数-前向后向算法
计算所有路径的总分面对的难题是要不要穷举所有路径。对于一个长度为N的序列,可能状态数为M,所有可能路径数为$M^N$,这是一个指数级的计算量。计算每条路径分数的计算量是$O(N)$,直接用穷举法计算所有路径总分的计算量是$O(N\cdot M^N)$。这个计算量是无法接受的。
《统计学习方法》p176写,前向算法是基于“路径结构”递推计算所有路径分数。前向算法高效的关键是局部计算前向概率,再递推到全局。前向算法的计算量是$O(N\cdot M^2)$,前向算法减少计算量的原因是:每一次递推计算直接利用了前一个时刻的计算结果,避免了重复计算。
对于$w_0 \to w_1$的局部路径。
先计算$w_0$所有状态到$w_1$单个状态0的分数之和,并更新$w_1$的状态0的状态分数。有M条局部路径,计算量是$O(M)$
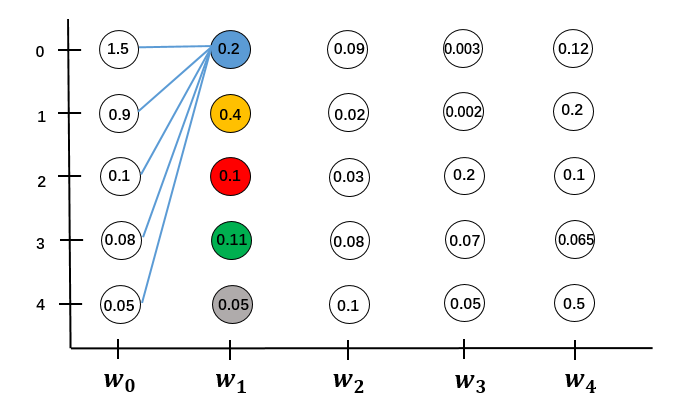
用同样的方法更新$w_1$所有状态的状态分数,这就是所有局部路径的分数。要计算M个状态,计算量是$O(M^2)$
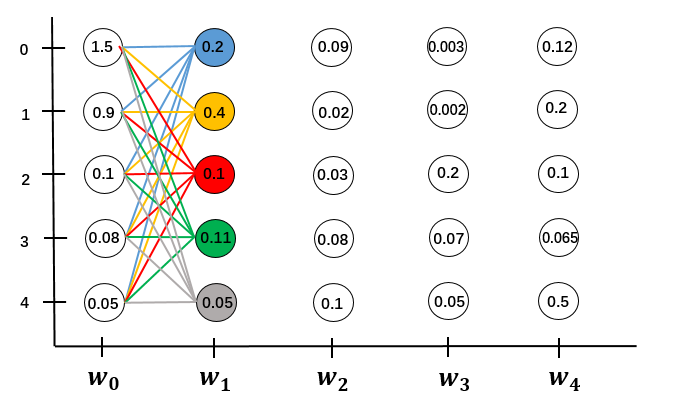
依次递推到全局。序列长度为N,总的计算量是$O(N \cdot M^2)$
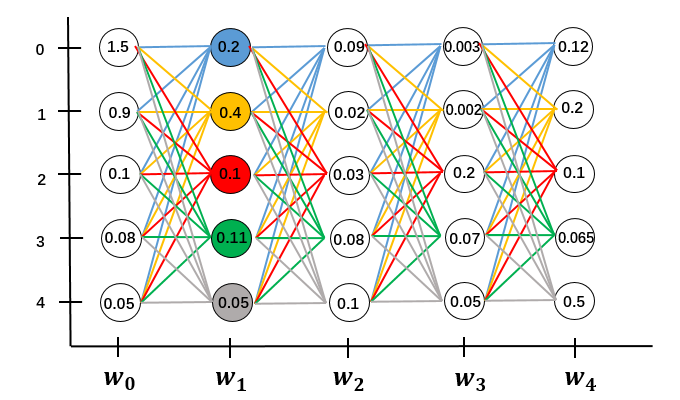
从图的角度解释了前向算法,我们再从数学计算的角度来看前向算法。简化一下问题,假设句子长度为3,$X = [w_0,w_1,w_2]$,只有2个类别[1,2]
我们引入两个变量previous和obs。previous存储前一时刻的计算结果,obs存储当前状态分数。
对于$w_0$:$$obs = [x_{01},x_{02}];previous = none$$
对于$w_0 \to w_1:$,$$previous = [x_{01},x_{02}],obs = [x_{11},x_{12}]$$
先扩展previous和obs:$$previous = \begin{pmatrix} x_{01}&x_{01}\x_{02}&x_{02} \end{pmatrix} \quad$$$$obs = \begin{pmatrix} x_{11}&x_{12}\x_{11}&x_{12} \end{pmatrix} \quad$$将previous和obs和转移矩阵相加:$$score =\begin{pmatrix} x_{01}&x_{01}\x_{02}&x_{02} \end{pmatrix} +\begin{pmatrix} x_{11}&x_{12}\x_{11}&x_{12} \end{pmatrix}+\begin{pmatrix} t_{11}&t_{12}\t_{21}&t_{22} \end{pmatrix}$$$$ = \begin{pmatrix} x_{01}+x_{11}+t_{11}&x_{01}+x_{12}+t_{12}\x_{02}+x_{11}+t_{21}&x_{02}+x_{12}+t_{22} \end{pmatrix}$$
score同列相加,更新previous:$$previous = [x_{01}+x_{11}+t_{11}+x_{02}+x_{11}+t_{21},x_{01}+x_{12}+t_{12}+x_{02}+x_{12}+t_{22}]$$
这样第二次迭代就完成了。用图来表示到目前为止的计算:
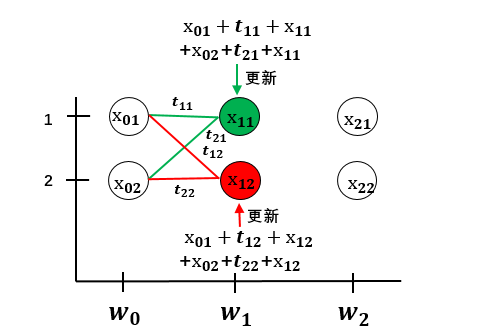
用同样的方法迭代递推,就可以得到所有路径的分数。
这样我们就计算出了负对数似然函数,也就是CRF模型的损失函数。
条件随机场的第二个基本问题是学习问题,给定训练集估计条件随机场的模型参数(转移矩阵)。我们可以通过最小化对数似然函数来求参数模型。可以用梯度下降法来实现。
维特比算法解码
条件随机场的第三个基本问题是预测问题,给出条件随机场的模型 和 输入序列x,求条件概率最大输出序列$y^*$。 也就是找出所有路径中得分最高的那条路径作为标注路径。与计算所有路径总分一样,我们面对的难题是要不要求出所有路径的分数。当然是不用的,我们用维特比算法来解码。
通信专业的同学一定知道大名鼎鼎的维特比算法,卷积码的译码就是用的维特比算法。
对于 $w_0 \to w_1$:
先计算$w_0$到$w_1$的状态1五条路径的分数,找出分数最大的一条保留下来,其他全都丢弃掉。计算量为$O(M)$
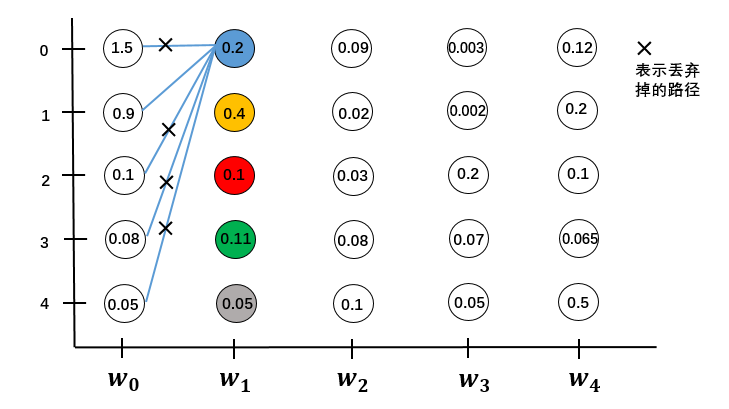
同样的找出$w_1$每个状态分数最大的一条路径,要计算$w_1$的5个状态,计算量为$O(M^2)$
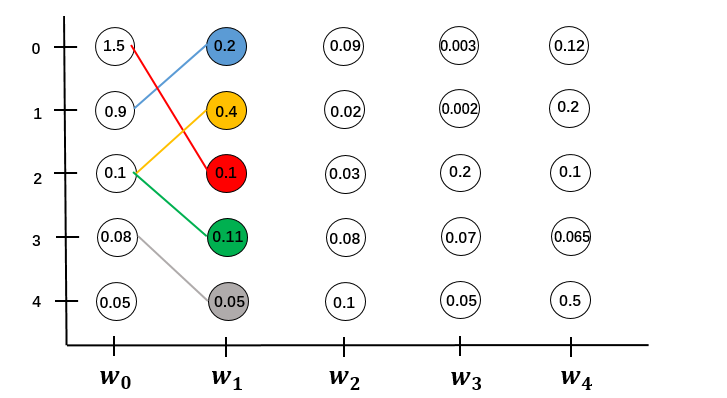
依次递推到全局。序列长度为N,计算量为$O(N \cdot M^2)$
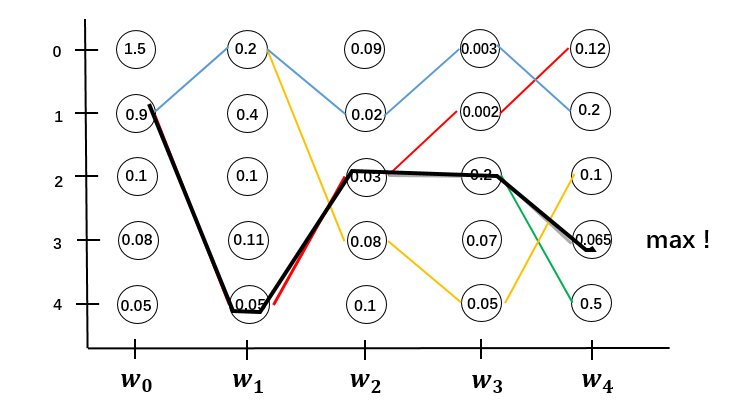
比较下前向算法与维特比算法的异同:
相同的地方在他们都面临要不要计算所有路径分数的问题,都是基于路径结构,用局部递推到全局。
不同的地方在于前向算法在更新previous的单个状态时是做求和sum运算,而维特比算法是做max运算,只保留分数最大的,丢弃掉其他路径。此外,维特比算法找到分数最大的路径后,还要反向递推
