读了博主Weng, Lilian的文章attention? attention!，是一篇很好的文章。打算按照这篇文章的思路，进行翻译，并添加自己的理解。
attention机制在深度学习中被广为使用，本文介绍attention机制的提出，不同的attention机制，及attention机制的进一步探索和应用。
why we need attention?从seq2seq模型谈起
seq2seq模型与14年提出(Sutskever, et al. 2014)，实现输入序列(source sequence)到输出序列(target sequence)的映射，这两个序列的长度都是可变的。序列到序列映射的任务包括机器翻译、问答系统、对话系统、摘要生成等。
用数学语言来定义序列到序列的任务，给定输入序列(source sequence) $X = \lbrace{ x_1,x_2,…,x_n \rbrace}$，需要生成输出序列(target sequence) $Y = \lbrace{ y_1,y_2,…,y_m \rbrace}$，其中source sequence长度为$n$,target sequence长度为$m$。
seq2seq模型基于encoder-decoder框架，包括2个部分：
encoder将source sequence编码（映射）为一个固定维度的向量表示(context vector,或称为sentence embedding)，我们希望这个向量表示可以很好的表示source sequence的意思。
encoder可以采用卷积神经网络CNN，也可以采用循环神经网络RNN，但用的更多的效果也更好的还是RNN。通常使用LSTM 或 GRU。
encoder RNN的隐藏状态更新公式为：$$\begin{gather}h_t = f(h_{t-1},x_t)\end{gather}$$其中$h_t$为RNN在时间步t的隐藏状态，f为LSTM 或GRU.
对于长度为n的source sequence，一个词接一个词地输入RNN后，可以得到n个隐藏状态$(h_1,h_2,…,h_n)$，通常将最后一个时间步最后一个词对应的隐藏状态$h_t$作为source sequence的向量表示，也就是context vector，记为$c$。decoder根据source sequence的向量表示context vector，来一个词一个词的生成target sequence。
decoder采用单向RNN，decoder RNN隐藏状态的更新公式为:$$\begin{gather}s_t = f(s_{t-1},y_{t-1},c)\end{gather}$$其中$s_t$为decoder在时间步t的隐藏状态，$y_{t-1}$为target sequence中的上一个词，在train阶段，$y_{n-1}$为真实target sequence中的上一个词，在infer阶段，$y_{t-1}$为预测输出的上一个词；c为context vector。
时间步t，隐藏状态$s_t$再经过线性层和softmax得到在词表上的概率分布，将概率最大的词作为prediction word $y_t$。迭代循环直到输出整个target sequence。
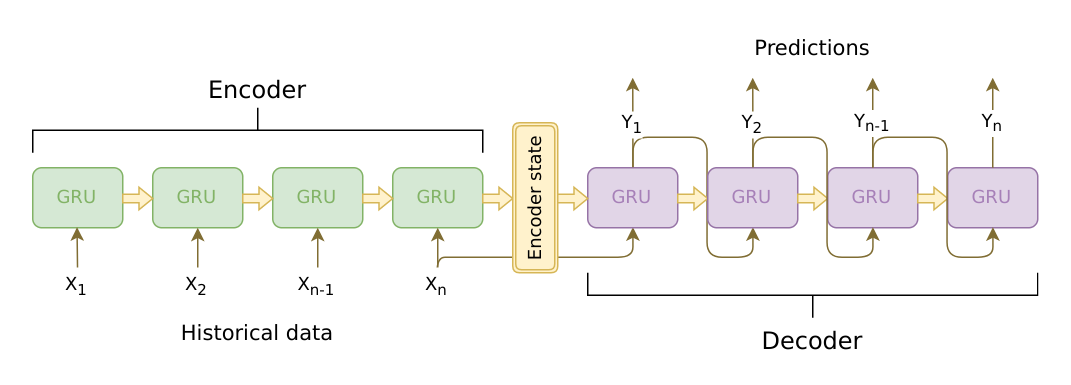
我们可以看到当生成不同的$y_t$时，所依据的context vector都是固定不变的。固定的context vector有一个缺点是：当encoder编码完整个source sequence时，会偏向于最近的词，而遗忘了距离更远的最开始的一些词。(Bahdanau et al., 2015)提出了attention机制来解决这个问题。
attention机制:born for Translation
attention机制最先在机器翻译(neural machine translation,NMT)任务上提出。从解决长期依赖问题的角度，attention可以实现长距离的记忆；从注意力的角度，attention机制可以实现对齐(alignment)，用更多的注意力关注到相关的部分，而忽略或低注意力关注到不相关的部分。
上文中提到，在生成不同的$y_t$时，直接将encoder最后一个时间步的隐藏状态$h_n$作为固定context vector。不同于这种方法，attention机制将所有encoder隐藏状态$\lbrace{ h_1,h_2,…,h_n }\rbrace$的加权和作为context vector，这样在每个时间步t生成$y_t$时，所依据的context vector都是专门针对于$y_t$的。
一方面，context vector可以获取到所有隐藏状态，也就是整个source sequence的信息，这样就可以实现长距离的记忆。另一方面，source sequence 与target sequence之间的语义对齐(aligenment)是也是通过context vector实现的。在计算时间步t生成$y_t$对应的context vector $c_t$的计算需要三个部分的信息：
- 所有的encoder隐藏状态： $\lbrace{ h_1,h_2,…,h_n }\rbrace$
- 上个时间步t-1的decoder 隐藏状态： $s_{t-1}$
- source与target之间的alignment.
](/images/44.png)
Fig.2.有attention机制的encoder-decoder模型，来源:[Bahdanau et al., 2015.](https://arxiv.org/pdf/1409.0473.pdf)
attention的数学定义
在计算时间步t生成$y_t$对应的context vector $c_t$时，encoder的所有隐藏状态为 $\lbrace{ h_1,h_2,…,h_n }\rbrace$，时间步t-1的decoder隐藏状态为 $s_{t-1}$，decoder RNN的隐藏状态更新公式变为：$$\begin{gather}s_t = f(s_{t-1},y_{t-1},c_t)\end{gather}$$ context vector $c_t$为encoder hidden state的加权和：
$$c_t = \sum_{i=1}^{n}\alpha_{t,i}h_i$$ $$\alpha_{t,i} = softmax(\beta_{t,i}) = \frac{exp(\beta_{t,i})}{\sum_{j = 1}^{n}exp(\beta_{t,j})}$$ $$\beta_{t,i} = score(s_{t-1},h_i)$$
其中权重$\alpha_{t,i}$是时间步t生成$y_t$与隐藏状态$h_i$之间的score，从某种意义上说，$h_i$可以看作是$x_i$的表示，也可以看作是$\lbrace{x_1,x_2,…,x_{i}}\rbrace$的表示。因此，$\alpha_{t,i}$可以看作是$y_t$与$x_i$之间联系（相关性）的score。所有权重$\lbrace{\alpha_{t,1},\alpha_{t,2},…,\alpha_{t,n}}\rbrace$衡量了生成$y_t$时应该如何关注到所有的encoder hidden state。
score()为打分函数，有多种计算方法，下文会详细介绍。在Bahdanau et al., 2015.中，score()采用前馈神经网络，采用非线性激活函数$tanh()$,score()的数学形式为：$$score(s_{t},h_i) = v_a^\top tanh(W_a[s_t;h_i])$$
其中$v_a,W_a$是可训练参数。
attention权重可视化矩阵很直观地表明了source words与target words之间的关联关系:
各种attention机制
汇总
下表总结了使用比较广泛的attention机制，及其对应的alignment score function。
| 名字 | alignment score funtion | 来源 |
|---|---|---|
| content-based attention | $score(s_t,h_i) = cosine(s_t,h_i)$ | Graves2014 |
| concat/additive | $score(s_{t},h_i) = v_a^\top tanh(W_a[s_t;h_i])$ | Bahdanau2015 |
| location-based | $\alpha_{t,i} = softmax(W_as_t)$ 将alignment简化为只依赖于target position |
Luong2015 |
| general | $score(s_{t},h_i) = s_t^\top W_ah_i$ | Luong2015 |
| dot-product | $score(s_{t},h_i) = s_t^\top h_i$ note:当general attention的$W_a$为单位矩阵时，就退出为dot-product attention |
Luong2015 |
| scaled dot-product(*) |
$score(s_{t},h_i) = \frac{s_t^\top h_i}{\sqrt{n}}$ note:跟dot-product attention很像，n是encoder hidden state $h_i$的维度 |
Vaswani2017 |
下表列出了更广范畴上的attention机制。
| 名字 | 定义 | 来源 |
|---|---|---|
| self attention(&) | 将input sequence的不同部分联系起来，只用到input sequence本身，而不用target sequence。 可以使用上表中的所有score function，只要将target sequence替换为input sequence即可。 |
Cheng2016 |
| global/soft attention | context vector是整个input sequence的加权和，注意到整个input sequence | Xu2015 |
| local/hard attention | context vector是局部input sequence的加权和，注意到局部input sequence | Xu2015， Luong2015 |
self-attention
self-attention,最先在Cheng2016提出称为”intra-attention”，后来在大作attention is all you need中发挥了更大的影响力。self-attention将同一个sequence的不同位置的tokens联系起来，建模tokens之间的关系，计算这个sequence的向量表示。[Cheng2016]提出self-attention的动机是什么呢？
我们先看以下LSTM的局限。LSTM在编码sequence的向量表示时，隐藏状态更新公式为：$$h_t = f(h_{t-1},x_t)$$从这个更新公式可以看到：在给定$h_t$的条件下，$h_{t+1}$与之前的状态$\lbrace{h_1,h_2,…,h_{t-1}}\rbrace$及之前的tokens $\lbrace{x_1,x_2,…,x_t}\rbrace$是条件独立的。LSTM的潜在假设是当前状态$h_t$包含了之前所有tokens的信息，这相当于假设LSTM有无限大的memory，这个假设实际上是不成立的。实际上LSTM会偏向于更近的tokens，而逐渐遗忘距离更远的tokens。另一方面，LSTM在编码token的隐藏状态时，没有建模tokens之间的关系。而这恰恰就是self-attention要解决的问题，也就是self-attention的核心思想：在计算sequence的向量表示时，引入tokens之间的关系。
接下来看self-attention的数学表示。对于sequence $\lbrace{x_1,x_2,…,x_n}\rbrace$，每个token $x_t$分别对应一个hidden vector 和memory vector。当前的memory tape $C_{t-1} = \lbrace{c_1,c_2,…,c_{t-1}}\rbrace$，hidden state tape为$H_{t-1} = \lbrace{h_1,h_2,…,h_{t-1}}\rbrace$。self-attention计算$x_t$与$\lbrace{x_1,x_2,…,x_{t-1}}\rbrace$之间的关系：$$\beta_{t,i} = score(x_t,h_i) = v^\top tanh(W_hh_i,W_xx_t,W_{\tilde{h}}\tilde{h_{t-1}})$$ $$\alpha_{t,i} = softmax(\beta_{t,i}) ;i\in[1,t-1]$$
attention权重$\alpha_{t,i}$是t时间步x_t在之前的tokens $\lbrace{x_1,x_2,…,x_{t-1}}\rbrace$对应的hidden vector上的概率分布。
来源:[Cheng2016](https://arxiv.org/pdf/1601.06733.pdf)
比较一下self-attention机制与传统attention机制的区别：
- 传统的attention机制是将target sequence与source sequence联系起来，attention权重$\lbrace{\alpha_{t,1},\alpha_{t,2},…,\alpha_{t,n}}\rbrace$是在encoder hidden states $\lbrace{h_1,h_2,…,h_n}\rbrace$上的概率分布。而self-attention是将同个sequence不同位置的tokens联系起来，attention权重$\alpha_{t,i}$是t时间步$x_t$在之前的tokens $\lbrace{x_1,x_2,…,x_{t-1}}\rbrace$对应的hidden vector上的概率分布。
- 传统的attention机制常与RNN联合使用，在transformer中self-attention可以与RNN解耦开（也就是分开使用），单独用self-attention也可以编码sequence的表示向量。
soft vs hard attention
Show, Attend and Tell,Kelvin Xu2015将attention机制用到了”给图片生成描述”的任务，第一次明确区分了hard attention与soft attention，区分的依据是attention是关注到整张图片，还是图片的局部。
- soft attention：attention关注到整张图片，或者是整个序列。alignment 权重$\alpha_{t,i}$是在整个序列上的概率分布。就像普通的attention一样。
- 好处：模型是可微的。
- 坏处：计算量比较大。
- hard attention：attention关注到图片的局部，或者是序列的一部分。
- 好处：减少了计算量。
- 坏处：模型不可微，需要用更复杂的技术，比如强化学习或者方差缩减来训练模型。Luong2015
global vs local attention
Luong2015在NMT任务上提出了global 和local attention的概念。区分的依据是attention是关注到整个序列，还是关注到序列的一部分。
- global attention。 类似于soft attention，关注到整个序列。这里比较下Luong2015的global attention与Bahdanau2015中attention的区别。
- Bahdanau2015中attention的计算路径是：$s_{t-1} \to \alpha_{t} \to c_t \to s_t$
$$\beta_{t,i} = score(s_{t-1},h_i)$$ $$\alpha_{t,i} = softmax(\beta_{t,i})$$ $$c_t = \sum_{i = 1}^{n}\alpha_{t,i}h_i$$ $$RNN更新公式：s_t = f(s_{t-1},y_{t-1},c_t)$$ $$y_t预测公式:p(y_t|y_{< t},x) = g(y_{t-1},c_t,s_t)$$ - Luong2015的global attention的计算路径是：$s_t \to \alpha_{t} \to c_t \to \tilde{s_t}$
$$\beta_{t,i} = score(s_{t},h_i)$$ $$\alpha_{t,i} = softmax(\beta_{t,i})$$ $$c_t = \sum_{i = 1}^{n}\alpha_{t,i}h_i$$ $$RNN更新公式：s_t = f(s_{t-1},y_{t-1},c_t)$$ $$\tilde{s_t} = tanh(W_c[c_t,s_t])$$ $$y_t预测公式:p(y_t|y_{< t},x) = softmax(W_s\tilde{s_t})$$
- Bahdanau2015中attention的计算路径是：$s_{t-1} \to \alpha_{t} \to c_t \to s_t$
- local attention。是soft 与hard attention的结合，关注到序列的一部分。对hard attention进行改进，使得模型可微，训练和计算变得更容易。改进的方法如下：
- 对于时间步t的target token $y_t$先用模型预测，生成一个对齐的位置$p_t$，
- 再根据固定窗口大小内$[p_t - D,p_t + D]$的encoder hidden state来计算context vector。D是窗口大小，是按经验定义好的。
](/images/47.png)
来源：[Luong2015](https://arxiv.org/pdf/1508.04025.pdf)
pointer network
对于输出序列的类别数依赖于输入序列的长度的问题，seq2seq模型或神经图灵机不能解决。因为这类问题中，输出的类别数是可变的，而seq2seq模型的decoder只能在固定数目的类别上生成一个概率分布。Vinyals2017提出了pointer network（Pr_Net）来解决输出词表可变的问题。pointer network实际上是以attention为基础的。
我们比较下attention机制与pointer network的区别。
记输入序列$X = \lbrace{x_1,…,x_n}\rbrace$,输出序列$Y = {y_1,…,y_m}$，$y_j$是X的位置索引，$y_i \in [1,n] $。
encoder的所有hidden state为$\lbrace{h_1,h_2,…,h_n}\rbrace$，decoder在时间步t的隐藏状态为$s_t$，则：
- attention机制用alignment权重来计算context vector：
$$\beta_{t,i} = score(s_t,h_i) = v^\top tanh(W_ss_t,W_hh_i); i \in [1,n]$$ $$\alpha_{t,i} = softmax(\beta_{t,i})$$ $$c_t = \sum_{i=1}^{n}\alpha_{t,i}h_i$$ - pointer network则用alignment权重在作为在输入序列上的概率分布，将输入序列中的token直接复制到输出序列中：
$$\beta_{t,i} = score(s_t,h_i) = v^\top tanh(W_ss_t,W_hh_i); i \in [1,n]$$ $$p(y_i|y_{< i},X) = softmax(\beta_{t,i})$$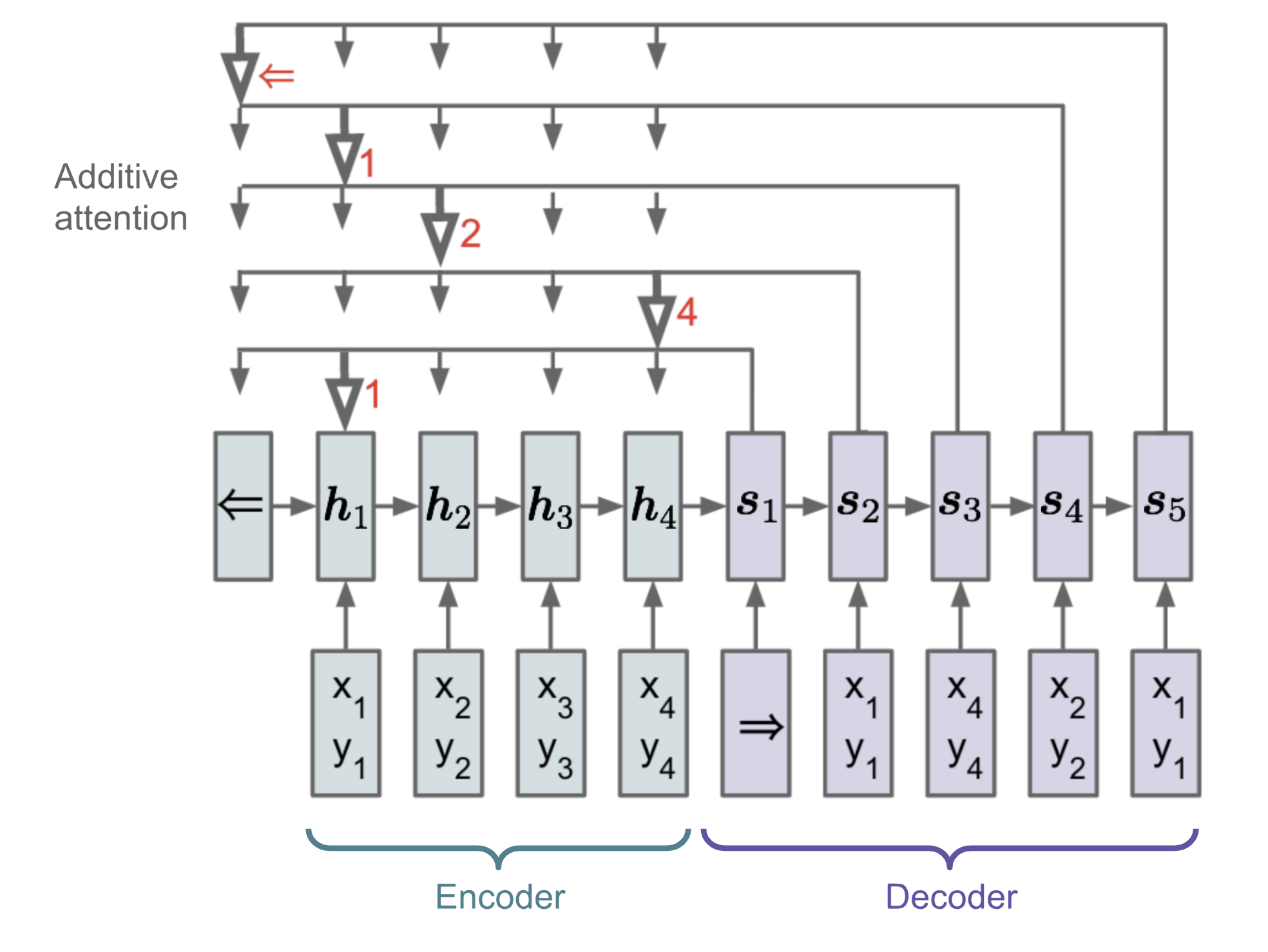
Fig.6.Pointer Network model
来源:[Vinyals2017](https://arxiv.org/abs/1506.03134)
pointer network解决OOV问题
什么是OOV（out of vocabulary）问题？在序列（source sequence）到序列（target sequence）的映射问题（对话系统，问答系统）中，会根据训练集语料来构建词表，根据完成$word \to index \to embedding$的向量化表示。而在测试集的source sequence中难免会出现一些词表中没有的词，通常会将这些out of vocabulary的词映射到一个特定的字符”UNK”，而decoder在生成response时也可能生成”UNK”这个特殊字符。这就是OOV问题。
pointer network是解决OOV问题的有效方法。当source sequence中出现不在词表中的词时，pointer network可以直接将这个生词从输入序列复制到输出序列中。Abigail See2017就用了pointer network来解决OOV问题。
记时间步t decoder的隐藏状态为$s_t$,对应的context vector为$c_t$,alignment权重为$\alpha_{t,i},i \in [1,n]$
- 在词汇表上的概率分布为:$p_{vocab} = softmax(W[s_t,c_t] + b)$
- 在输入序列的概率分布为:$p_{ptr} = \alpha_{t,i} = softmax(\beta_{t_i})$
- 选择开关为: $p_{gen} = sigmoid(W_ss_t + W_cc_t + W_xx_t + b)$
为逻辑回归，取值为[0,1] - 最终在extend vocabulary上的概率分布为:$p(w) = p_{gen}p_{vocab} + (1-p_{gen})p_{ptr}$.
当$p_{gen}$为1时，从词汇表中生成word；当$p_{gen}$为0时，将输入序列的词复制到输出序列中。
](/images/48.png)
来源：[Abigail See2017](https://arxiv.org/abs/1704.04368)
类似的论文还有：CopyNet,Jiatao Gu2016
transformer
attention is all you need!(Vaswani, et al., 2017)提出了transformer。transformer也是基于encoder-decoder框架的，也可以看作是一个seq2seq模型。但不同于encoder和decoder都采用RNN的seq2seq模型，transformer完全依赖self-attention机制来计算input和output的向量表示，而不使用RNN或CNN。一般来说，attention机制是与RNN联合使用的，transformer把attention和RNN解耦开了，只使用attention机制。
为什么transformer用self-attention来编码input和output，而不使用RNN呢？
一方面，由RNN的更新公式$s_t = f(s_{t-1},x_t)$可以看到，RNN处理序列时是串行计算的，尤其是处理长序列时更费时间。不利于并行化，计算效率低。而transformer采用attention来编码计算向量，可以进行并行化计算，提高计算效率。
另一方面，RNN在编码长序列时，随着距离的增大，往往会偏向于最近的部分，而学习不到长期依赖。但self-attention机制不受距离的限制，可以有效地学习到长期依赖。
scaled dot-product attention与key,value,query
transformer的主要组件是multi-heads self-attenion mechanism，这个组件用到了scaled dot-product attention机制。一般地，attention机制将query和(key,value)映射为output，其中query,key,value,output都是vector。output是所有values的加权和，权重是通过计算query与对应key之间的关联度得到。
具体来说，将什么作为key,value,query？分两种情况，从框图可以直观的看到：
- 在encoder-decoder框架中，联系encoder与decoder的attention机制通常将encoder的所有hidden states乘以两个不同的矩阵$W^Q,W^K$分别作为keys和values。将decoder上一个时间步的hidden state作为query。
- 在encoder模块，self-attention机制将input词级别的向量表示乘以三个不同的矩阵$W^Q,W^K,W^V$分别作为query,key,value。进而计算input总的句子级别的向量表示。同样地，在decoder模块中self-attention机制将output词级别的向量表示分别乘以三个不同矩阵$W^Q,W^K,W^V$分别作为query,key,value。进而计算output总的句子级别的向量表示。
有了具体的key,value,query后，scaled dot-product attention机制怎么来计算output呢？
记query,key,value的矩阵形式分别为Q,K,V。query和key维度为$d_k$,value维度为$d_v$。则output的计算方式为：$$Attention(Q,K,V) = softmax(\frac{QK^\top}{\sqrt{d_k}})V$$
多种attention机制中，transformer为什么选择采用scale dot-product attention机制呢？
最常用的两种attention机制是dot-product和additive attention机制。dot-product attention用点乘来做打分函数，additive attenion将有一层隐藏层的前馈网络作为打分函数。理论上来说，这两种attention的计算复杂度是一样的；但实际上，dot-product attention计算更快，占用内存更小。因为dot-product attention机制可以采用高度优化的矩阵乘法代码。
当维度$d_k$较小时，这两种attention机制的效果是差不多的。当维度$d_k$更大时，additive attention的效果要好于dot-product attention。这可能是因为当维度$d_k$变大时，点乘的值变得过大，而softmax()函数在值过大的范围梯度是很小的，类似于梯度消失问题。因此，添加比例因子$\frac{1}{\sqrt{d_k}}$来减小点乘的值。
multi-head attention
并不是只用一次attention机制，将维度为$d_{model}$的key,value,query映射为output。而是将query,key,value映射到维度为$d_k,d_k,d_v$不同的子向量空间，并行的计算$h$次，分别得到output做concat操作，得到总的output。$h$为head的个数，也就是并行attention layer的层数。有关系$d_{model} = d_v \cdot h$，论文中采用$d_{model} =512,h=8,d_k = d_v = \frac{d_{model}}{h} = 64$ $$MultiHead(Q,K,V) = concat(head_1,head_2,…,head_h)W^O$$ $$where \quad head_i = Attention(QW_i^Q,KW_i^K,VW_i^V)$$ 其中$W_i^Q \in R^{d_{model} \cdot d_k},W_i^K \in R^{d_{model} \cdot d_k},W_i^V \in R^{d_{model} \cdot d_v},W^O \in R^{hd_{v} \cdot d_{model}}$
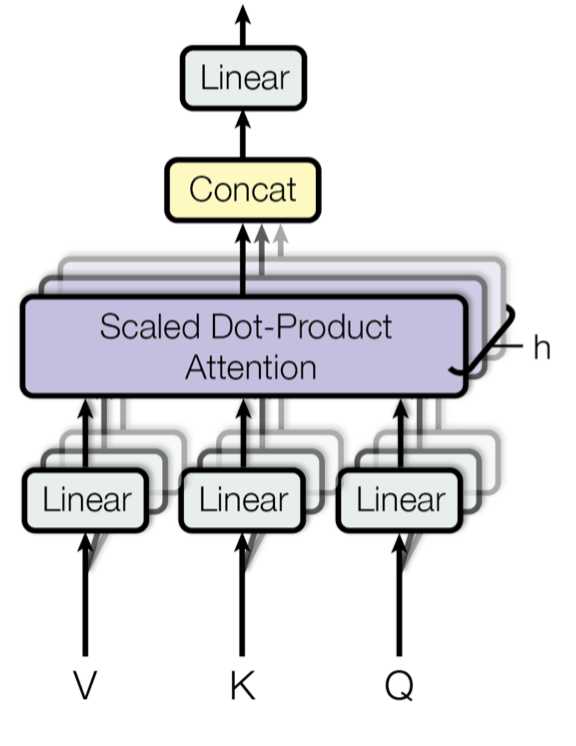
来源:Vaswani, et al., 2017
encoder
encoder将input text编码为基于attention的包含位置信息的向量表示。
- 由6个完全相同的层堆叠起来。
- 每一层包含两个子层。第一子层是multi-head attention层，第二层是一个简单的全连接层。
- 两个子层之间采用残差连接，并进行归一化。这样所有子层的输出都有相同的维度$d_{model} = 512$
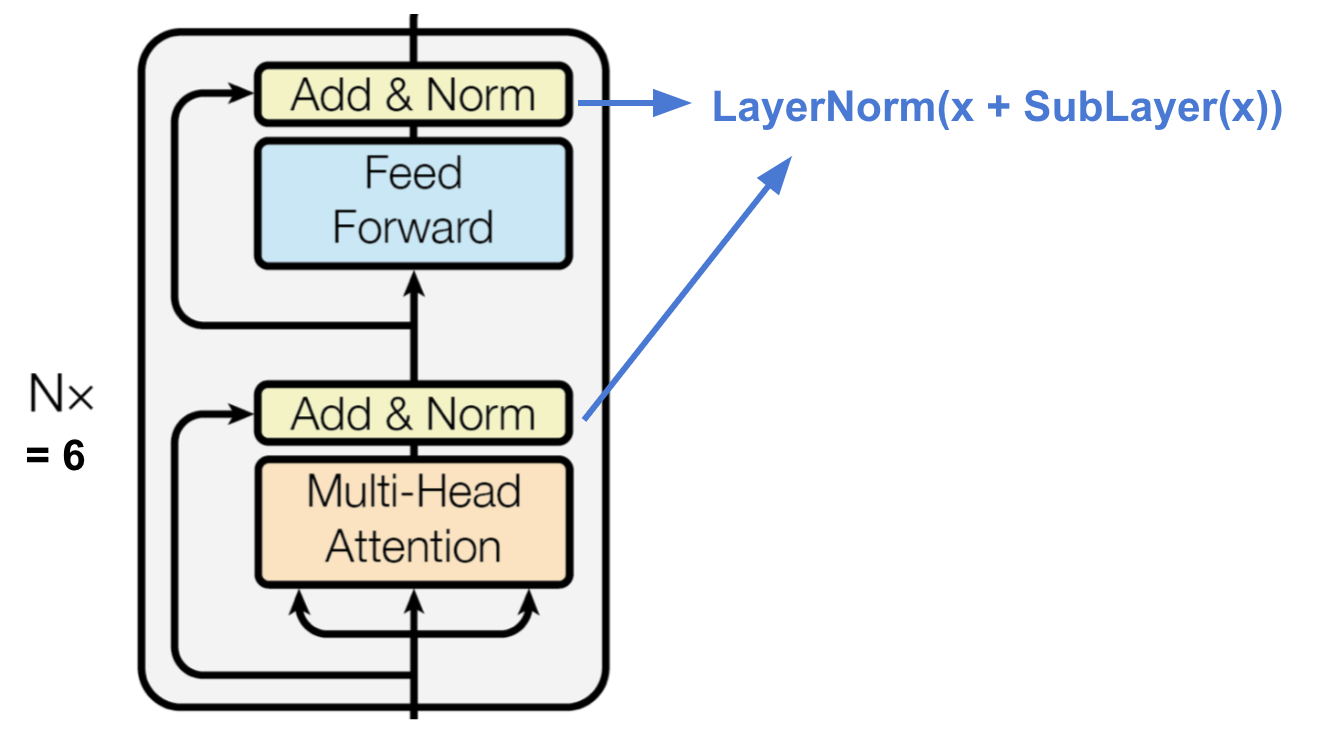
来源:Vaswani, et al., 2017
decoder
从encoder output得到总的context vector，并据此生成response。
- 与encoder相同，由6个完全相同的层堆叠起来。
- 每一层除了encoder中的两个子层外，还插入了一个multi-head layer来在所有encoder output上进行attention操作。
- 两个子层之间采用残差连接，并进行归一化。
- 第一个multi-head attention sub-layer进行mask操作，mask掉output当前时间步后所有的tokens。防止attention机制看到未来的信息。
来源:Vaswani, et al., 2017
transformer的总体结构
- input和output都先经过一个embedding layer得到各自的向量表示，维度为$d_{model} = 512$
- 由于self-attention不能像RNN一样自动地编码位置信息，因此需要额外地将位置信息添加到输入。
- 在最后decoder的输出外接一个线性层和softmax层。
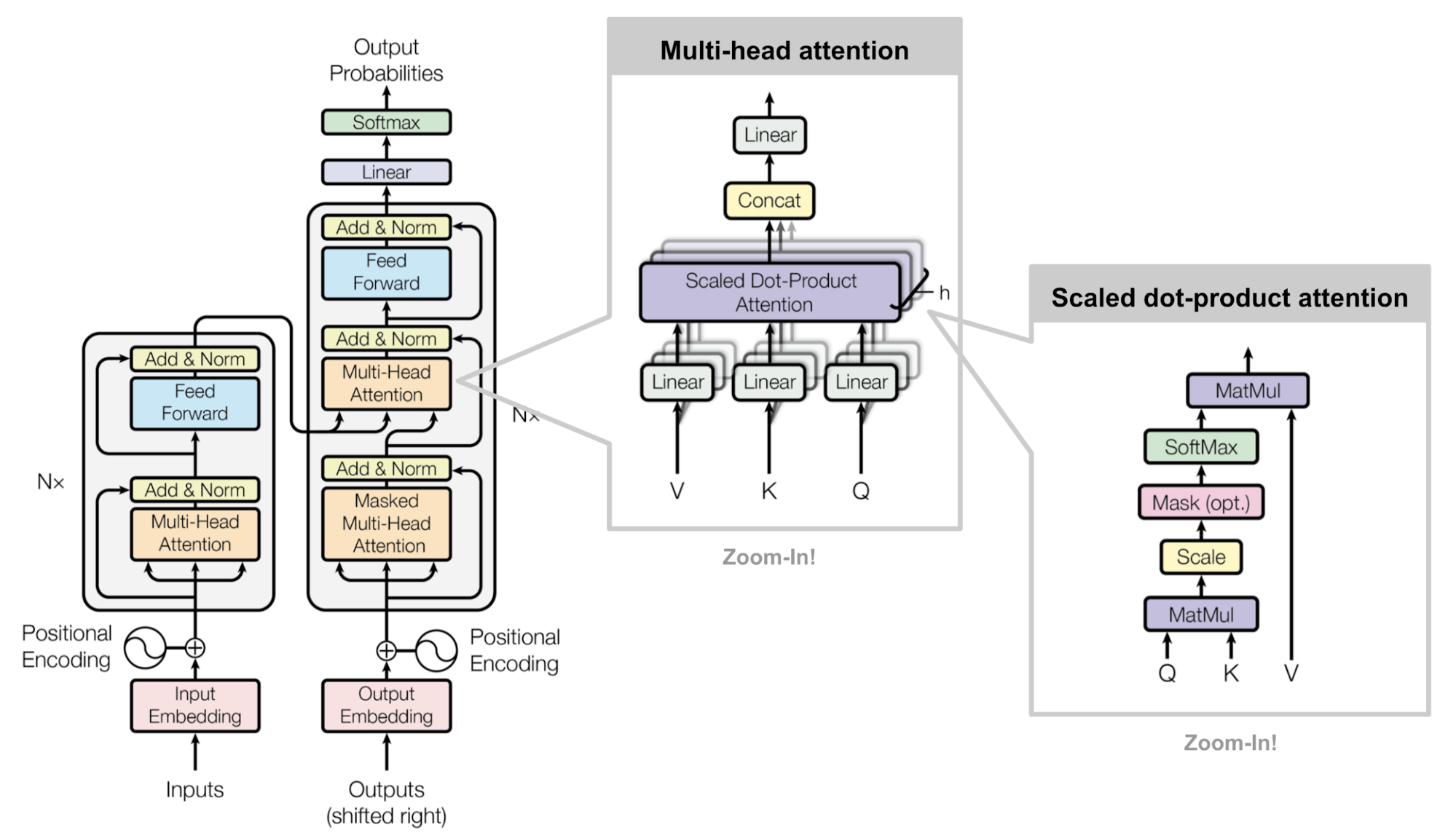
来源:Vaswani, et al., 2017
参考链接
- Attention? Attention! by Weng, Lilian
