介绍Memory Networks。
Neural Turing Machines-神经图灵机
Google DeepMind团队在Alex Graves2014提出Neural Turing Machines,第一次提出用external memory来提高神经网络的记忆能力。这之后又出现了多篇关于Memory Networks的论文。我们先看看Turing Machines的概念。
Turing Machines-图灵机
计算机先驱turing在1936年提出了Turing Machines这样一个计算模型。它由三个基本的组件:
- tape: 一个无限长的纸带作为memory,包含无数个symbols,每个symbol的值为0、1或”$\space$”。
- head: 读写头,对tape上的symbols进行读操作和写操作。
- controller: 根据当前状态来控制head的操作。
理论上Turing Machines可以模拟任何一个计算算法,不管这个算法多么复杂。但现实中,计算机不可能有无限大的memory space,因此Turing Machines只是数学意义上的计算模型。

Neural Turing Machines
Neural Turing Machines(NTM,Alex Graves2014)用external memory来提高神经网络的记忆能力。LSTM(Long and short memory)通过门机制有效缓解了RNN的’梯度消失和梯度爆炸问题’,可以通过internal memory实现长期记忆。当LSTM的internal memory的记忆能力有限,需要用external memory来提高神经网络的记忆能力。
Neural Turing Machines包含两个基本组件:a neural network controller和memory bank。memory是一个 $N\cdot M$阶的矩阵,包含N个向量,每个向量的维度是M。我们把每个memory vector称为memory location。controller控制heads对memory进行读写操作。
如何对memory matrix进行读写操作呢?关键问题是如何让读写操作是可微的,这样才能用梯度下降法来更新模型参数。具体来说,问题是让模型关于memory location是可微的,但memory locations是离散的。Neural Turing Machines用了一个很聪明的方法来解决这个问题:不是对单独某个memory location进行读写操作,而是对所有的memory locations进行不同程度的读写操作,这个程度是通过attention的权重分布来控制的。
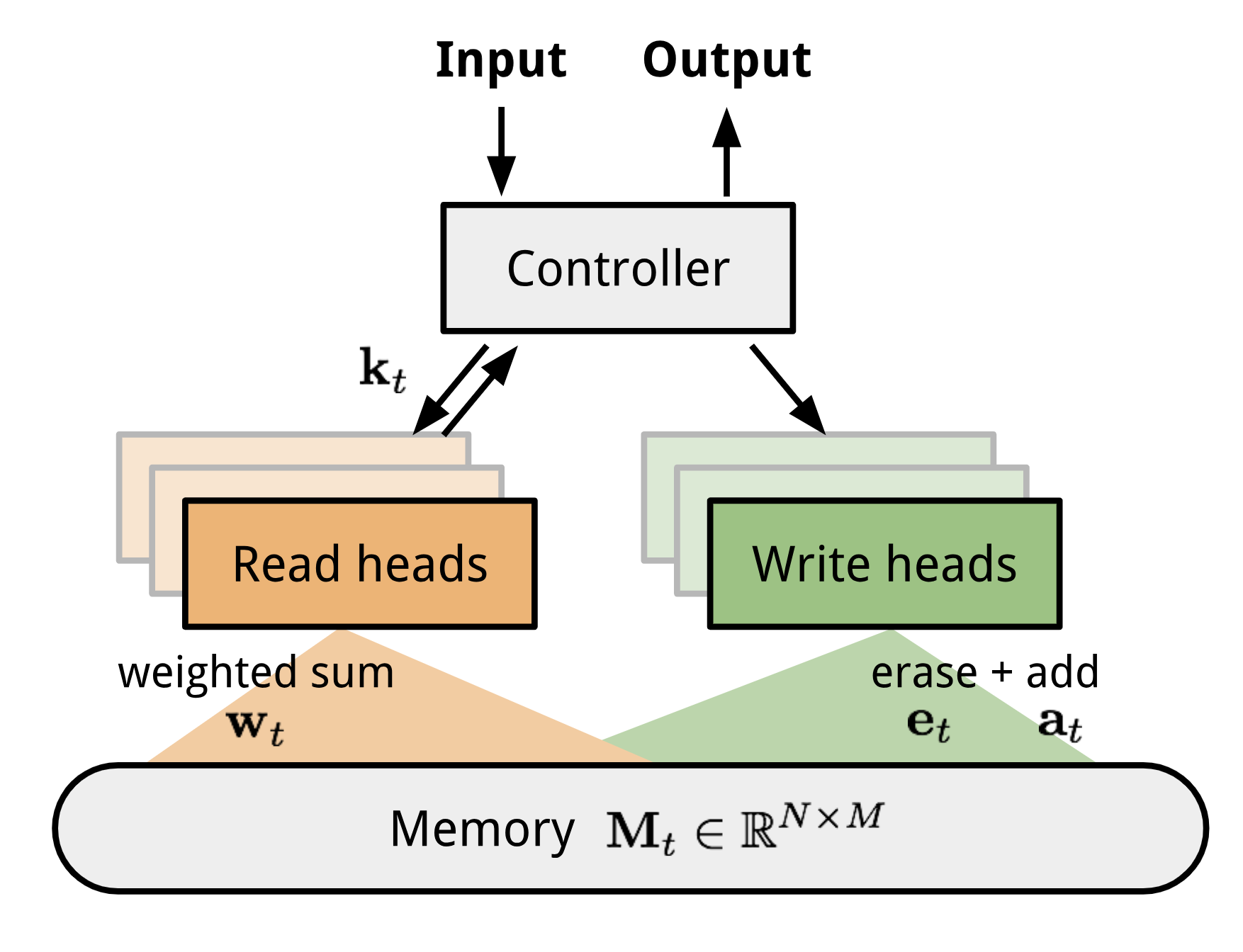
读操作
记时间步t memory matrix为$N\cdot M$阶矩阵$M_t$,$w_t$是在N个memory向量上的权重分布,是一个N维向量。则时间步t的read vector $r_t$为$$r_t = \sum_{i=1}^{N}w_t(i)\cdot M_t(i)$$ $$where: \sum_{i=1}^{N}w_t(i) = 1; 0 \le w_t(i) \le 1,\forall i $$其中,$w_t(i)$是$w_t$的第i个元素,$M_t(i)$是$M_t$的第i个行向量。
写操作
受LSTM门机制的启发,将写操作分成两步:先erase,再add。先根据erase vector $e_t$擦去旧的内容,再根据add vector $a_t$添加新的内容。
- 先erase:
在时间步t,attention权重分布为$w_t$,erase vector $e_t$是一个M维向量,每个元素取值[0,1],上一个时间步的memory vector为$M_{t-1}$。则erase操作为$$\tilde{M_{t}}(i) = M_{t-1}(i)[\vec{1}-w_t(i)e_t]$$ $\vec{1}$是一个M维的全1向量。对memory vector的erase操作是逐点进行的。当$e_t$的元素和memory location对应权重$w_t(i)$的元素值都是1时,memory vector $M_t(i)$的元素值才会置为0。如果$e_t$或$w_t(i)$的元素值为0时,memory vector $M_t(i)$的元素值保持不变。 - 再add:
每个write head会产生一个M维的add vector a_t,则:$$M_t(i) = \tilde{M_{t}}(i) + w_t(i)a_t$$至此,就完成了写操作。
寻址机制
进行读写操作前,要搞清楚对哪个memory location进行读写呢?这就是寻址。为了让模型关于memory locatios可微,Neural Turing Machines不是对某个单独的memory location进行读写操作,而是对所有memory locations进行不同程度的读写操作,这个程度就是由权重分布$w_t$来控制的。模型结合并同时使用了content-based和location-based两种寻址方式来计算这个权重分布$w_t$。具体地,权重计算分为以下几步:
- content-based addressing
时间步t,每个head产出一个M维的key vector $k_t$,通过$k_t$与memory vectors $M_t(i)$之间的相似性来计算content-based attention权重分布$w_{t}^{c}$。相似性是通过余弦相似度来衡量的。$$w_{t}^{c} = softmax(\beta_tK(k_t,M_t(i))) = \frac{\beta_tK(k_t,M_t(i))}{\sum_{j}K(k_t,M_t(j))}$$ $$K(u,v) = \frac{u\cdot v}{|u|\cdot |v|}$$
$\beta_t$可以放大或缩小权重的精度。 - 内插法
每个head产生一个interpolation gate $g_t$,取值[0,1]。content-based attention权重分布为$w_t^{c}$,上一个时间步的attention权重分布为$w_{t-1}$。则门控制的权重分布$w_t^g$为:$$w_t^g = g_tw_t^c + (1-g_t)w_{t-1}$$当$g_t$为0时,采用上一个时间步的权重分布$w_{t-1}$,当$g_t$为1时,采用content-based attention权重分布$w_t^c$。 - 循环卷积
对经过插值后的权重分布$w_t^g$进行循环卷积,主要功能是对权重进行旋转位移。比如当权重分布关注某个memory location时,经过循环卷积就会扩展到附近的memory locations,也会对附近的memory locations进行少量的读写操作。每个head产生的转移权重为$s_t$,循环卷积的操作为:$$\tilde{w_t(i)} = \sum_{j=0}^{N-1}w_t^g(i)s_t(i-j)$$
关于$s_t$的详细介绍可以见attention?attenion!;
循环卷积的详细介绍可以见Neural Turing Machines-NTM系列(一)简述 - 锐化
循环卷积往往会造成权重泄漏和分散,为了解决这个问题,需要最后进行锐化操作。$$w_t(i) = \frac{\tilde{w_t(i)^{\gamma_t}}}{\sum_j\tilde{w_t(j)^{\gamma_t}}}$$其中$\gamma_t >1$。至此,就得到了时间步t的权重分布$w_t$。可以根据这个权重分布$w_t$对memory matrix进行读写操作。
总结以下这4步操作。第一步content-based addressing根据输入得到关于memory locations的相似度;后三步实现了location-based addressing。第二步插值操作引入了上一个时间步的权重分布,对content-based 权重进行修正;第三步循环卷积将每个位置的权重向两边分散;第四步锐化操作将权重突出化,大的更大,小的更小。
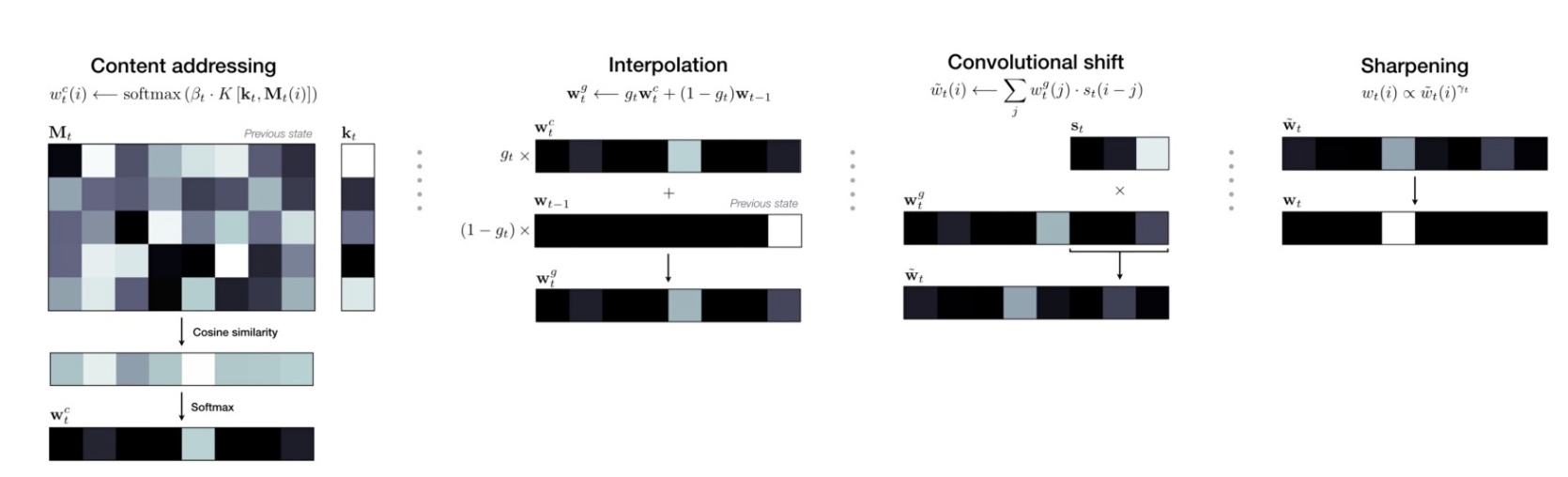
](/images/NTM-flow-addressing.png)
来源:[Alex Graves2014](https://arxiv.org/abs/1410.5401)
参考链接
- Attention and Augmented Recurrent Neural Networks
用动图直观地表现Neural Turing Machines的计算过程。推荐!👍 - 记忆网络之Neural Turing Machines,中文
- attention?attenion!
Memory Network
在Neural Turing Machines提出仅仅五天后,Facebook研究员Jason Weston发表了MEMORY NETWORKS。在QA系统的领域,应用memory network。虽然RNN或LSTM可以通过hidden state和weights来进行短期记忆,但它们的记忆能力是有限的。要实现长期记忆,需要memory network。
Memory Network的一般框架
memory network包括一个记忆单元memory,和四个基本组件:
- I(input feature map):
将input x进行向量化表示,编码为feature representation I(x)。 - G(generalization):
对memory进行写操作。根据input 来更新memory $m_i$。$m_i = G(m_i,I(x),m)$ - O(output feature map):
对memory进行读操作。根据input和memory生成output feature。$o = O(I(x),m)$ - R(response):
根据output feature o来生成response。
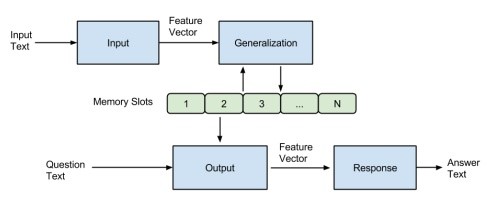
memory network框架的实现–MemNNs
在I模块将input $x_i$编码为$I(x_i)$后,G模块之间将$I(x_i)$保存到下一个空的memory slot中,而不更新旧的memory slots。真正实现inference的核心模块是O和R。
O模块在给定x的条件下,依次找到与x最相关的k个memory slots。论文中采用k = 2。先找到第一个最相关的memory slot:$$m_{o1} = \mathop{argmax}\limits_{i = 1,…,N} s_{o1}(x,m_i)$$其中$s_o()$是一个匹配函数,计算x与$m_i$之间的相关程度。接着,根据x和第一个memory找到下一个memory:$$m_{o2} = \mathop{argmax}\limits_{i = 1,…,N} s_{o2}([x,m_{o1}],m_i)$$将output feature o = $[x,m_{o1},m_{o2}]$作为R模块的输入。
R模块将词汇表中所有词与output feature进行匹配,选择匹配度最高的词作为response。这样生成的response只有一个词。$$r = \mathop{argmax}\limits_{w \in W}s_R([x,m_{o1},m_{o2}],w)$$其中$s_R()$是一个匹配函数。
匹配函数$s_O$和$s_R$都采用以下函数:$$s(x,y) = \Phi_x(x)^\top U^\top U \Phi_y(y)$$其中$\Phi_x(x),\Phi_y(y)$分别将x/y编码为向量。
目标函数
在训练阶段采用最大边缘目标函数,设对于question x,真实的label为r,对应的memory为$m_{o1},m_{o2}$。则最大边缘目标函数为:$$\sum_{m_i\ne m_{o1}}max(0,\gamma - s_{O1}(x,m_{o1}) + s_{O1}(x,m_i)) + $$ $$\sum_{m_j\ne m_{o2}}max(0,\gamma - s_{O2}([x,m_{o1}],m_{o2}) + s_{O2}([x,m_{o1}],m_j)) + $$ $$\sum_{r’ \ne r}max(0,\gamma - s_{R}([x,m_{o1},m_{o2}],r) + s_{R}([x,m_{o1},m_{o2}],r’))$$
由于argmax()函数的存在,这个模型是不可微的。而且中间过程找到相关memory需要监督,这个模型不是端到端的。
总的来说,这个memory network是一种普适性的架构,是很初级很简单的,很多部分还不完善,不足以应用具体的任务上。不过,通过多跳方式找到相关memory的思路是很值得学习的。
End-to-End Memory Network
Jason Weston作为三作的Sainbayar Sukhbaatar2015对Memory network工作的改进,主要改进是实现了端到端,减少了监督。End-to-End Memory Network采用soft attention而不是hard attention来read memory,因此是端到端的。另外不需要对相关memory进行监督。提高memory network的可用性。
假设多个句子input $x_1,…,x_n$作为memory,对于query q,输出对应的answer a。给定query q,经过多跳找到相关的memory,并生成对应的answer a。
single layer
给定input $x_1,x_2,…,x_n$,采用两个不同的embedding matrix A和C分别编码为向量$\lbrace{m_1,…,m_n}\rbrace$,$\lbrace{c_1,…,c_n}\rbrace$,分别对应attention机制的keys和values。将query q经过embedding matrix B编码为向量表示u。
采用dot-product attention计算权重:$$p_i = softmax(u^\top m_i) = \frac{exp(u^\top m_i)}{\sum_{j}exp(u^\top m_j)}$$
则memory representation为:$$o = \sum_{i}p_i m_i$$
根据u和o来进行预测:$$\hat{a} = softmax(W (o + u))$$
通过最小化a与$\hat{a}$之间的交叉熵来训练模型参数A,B,C,W。这个single layer end-to-end Memory network是简单而直观的。核心是用soft attention来read memory,找到相关的memory,并进行inference。](/images/mem.png)
来源:[Sainbayar Sukhbaatar2015](http://arxiv.org/abs/1503.08895)
multi layers
将K层single layer进行stack得到K层memory network,进行K跳memory查询操作。具体地stack方式为:
- 将第k层的输入$u^k$和memory representation $o^k$相加作为第k+1层的输入:$$u^{k+1} = u^k + o^k$$
- 每一层都有单独的embedding matrix $A^k$和$C^k$
- 最后一层的预测输出为:$$\hat{a} = softmax(W u^{K+1}) = softmax(W(u^K + o^K))$$
为了减少参数量,有两种方法:
- adjacent:
让相邻层的embedding matrix A=C,共享参数。即:$C^k = A^{k+1}$,对第一层有$A^1 = B$,最后一层有:$C^K = W$。这样就减少了一半的参数量。 - RNN-like:
跟RNN一样,采用完全参数共享的方法,$A^1 = A^2 = … = A^K$;$C^1 = C^2 = … = C^K$。参数数量大大减少导致模型效果变差,在层与层之间添加一个线性映射:$u^{k+1} = Hu^k + o^k$
key-value Memory Networks
Jason Weston作为作者之一的Alexander Miller2016在End-to-End Memory networks的基础上继续推进,可以更好的通过memory来编码和利用先验知识,并且具体地应用到了QA系统中。
作为memory的先验知识可以是结构化的三元组知识库,也可以是非结构化的文本。
- 三元组知识库。三元组的形式是”实体-关系-实体”,或”主语-谓语-宾语”。三元组知识库的优点是结构化的,便于机器处理。但缺点是与一句完整的话比较,三元组缺少了一些信息。由于三元组知识库是人工构建的,难免会有覆盖不到的知识,对于某个问题可能知识库中根本就没有对应的知识。另外,三元组中的实体可以有多种不同的表达,比如知识库中有三元组”中国-首都-北京”。当问题是“中华人民共和国的首都是?”时,可能就不能很好地回答。
- 像“维基百科”这样的非结构化文本。优点时覆盖面广,几乎包含所有问题的知识。缺点是非结构化的,有歧义,需要经过复杂的推理才能找到答案。
作为先验知识的memory是(key,value)形式的。
- key memory用于寻址(addressing/lookup)阶段,通过计算query与key memory的相关程度来计算attention权重,因此在设计key memory时,key memory的特征应该更好地匹配query。
- value memory用于read阶段,将value memory的加权和作为memory总的向量表示,因此在涉及value memory时,value memory的特征应该更好地匹配response。
比较一下end-to-end memory network与key-value memory network的区别:
- 前者是将相同的输入经过两个不同的embedding matrix编码分为作为key memory和value memory。而后者可以将不同的知识(key,value)分别编码为key memory和value memory,可以更灵活地利用先验知识。
- 后者的每个hop之间添加了用$R_j$来进行线性映射。
模型结构
在问答系统中,记memory slots为$(k_1,v_1),…,(k_M,v_M)$,问题query为x,真实回复为a,预测回复为$\hat{a}$。$\Phi_{X},\Phi_{Y},\Phi_{K},\Phi_{V}$分别是x,a,key,value的embedding matrix,将文本编码为向量表示。
则单次memory的寻址和读取可以分为三步:
- key hashing:
当知识库很大时,这一步是非常必要的。根据query从知识库中检索筛选出相关的facts $ (k_{h_1},v_{h_1}),(k_{h_2},v_{h_2}),…,(k_{h_N},v_{h_N})$,筛选条件可以是key中至少包含query中一个相同的词(去除停用词)。这一步可以在数据预处理时进行,直接将query和相关的facts作为模型的输入。 - key addressing(寻址阶段)
计算query与memory的相关程度来分配在memory上的概率分布:$$p_{h_i} = softmax(A\Phi_{X}(x) \cdot A\Phi_{K}(k_{h_i}))$$其中$\Phi$将文本编码为D维向量,A是一个$d\times D$的可训练矩阵。 - value reading:
将value的加权求和作为memory总的向量表示。$$o = \sum_{i}p_{h_i}A\Phi_{V}(v_{h_i})$$
memory的读取过程是由controller神经网络通过query $q = A\Phi_{X}(x)$来控制的。模型会利用query $q$与上一跳(hop)的$o$来更新query,进而迭代地寻址和读取memory,这个迭代的过程称为多跳(hops)。
用多跳方式来迭代地寻址和读取memory,可以这样来理解:浅层神经网络可以学习到低级的特征,随着神经网络层数增多就可以学习到更高级的特征。类比CNN处理人脸图片时,第一层可以学习到一些边缘特征,第二层可以学习到眼睛、鼻子、嘴巴这样的特征,最后一层得到整个人脸的特征。同样地,用多跳方式来寻址和读取memory,可以得到更相关更突出的memory,同时可以起到推理的作用。
query的更新公式为:$$q_2 = R_1(q + o)$$其中R是一个$d\times d$的可训练矩阵。每一跳使用不同的矩阵$R_j$。
则第j跳更新query后,寻址阶段的计算公式为$$p_{h_i} = softmax(q_{j+1}^\top \cdot A\Phi_{K}(k_{h_i}))$$
在经过H跳之后,用controller神经网络的最终状态进行预测:$$\hat{a} = argmax_{i=1,…,C}softmax(q_{H+1}B\Phi_{y}(y_i))$$其中B是一个$d\times D$的可训练矩阵,形状跟A一样。$y_i$可以是知识库中的实体,或者候选句子。
模型的目标函数为预测回复$\hat{a}$与真实回复$a$之间的交叉熵,用梯度下降的方法来更新模型参数:$A,B,R_1,…,R_H$
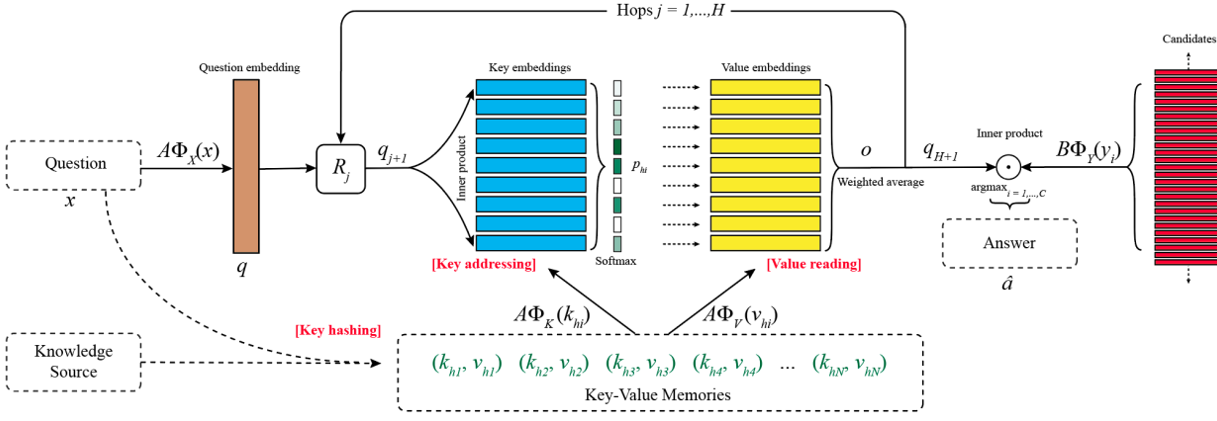
来源:Alexander Miller2016
key-value的选择与编码方式
论文根据不同形式的先验知识,提出了key-value不同的编码方式:
- 知识库三元组。三元组形式为”subject-relation-object”,将”subject-relation”作为寻址的key,将”object”作为记忆的value。
- sentence level。直接将句子的词袋向量表示作为key和value,key和value是一样的。每个memory slot存一个句子。
- window level。以大小为W的窗口对文档进行分割(只保留中心词为实体的窗口),将单个窗口内的词作为寻址的key,将窗口的中心词作为value。
