【来源】：NAACL2019
【链接】：https://arxiv.org/pdf/1810.10647.pdf
【代码、数据集】：https://github.com/DineshRaghu/multi-level-memory-network

已有工作中，端到端的任务型对话系统采用memory network来结合外部的知识库(knowledgt base) 和 对话历史(context)。为了使用从跑一趟 network，通常将二者放在同一个memory中。这样带来的问题是：memory变得太大，模型在读取memory时需要区分外部知识库和对话历史，并且在memory上的推理变得很难。为了解决这个问题，论文将外部知识库和对话历史区分开，另外，将外部知识库保存为分层的memory。

模型结构

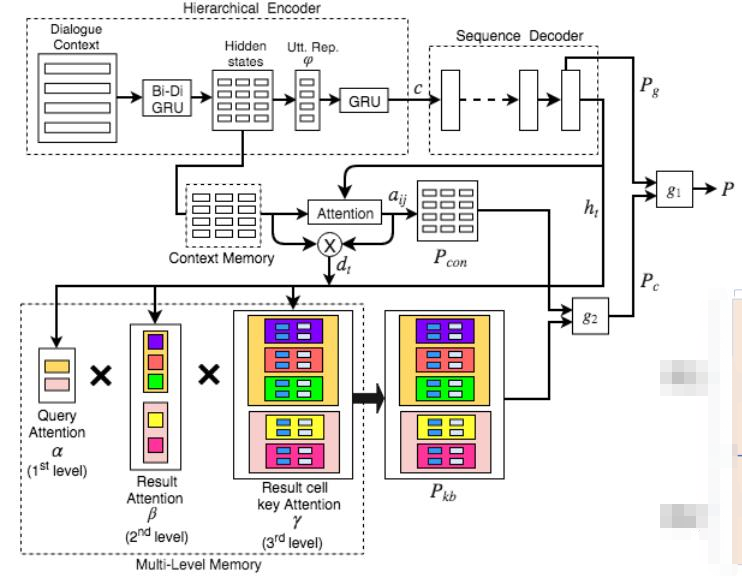
模型主要包括三个部分。

  • 分级encoder：
    分别编码对话历史中的句子。
  • milti-level memory
    保存了目前为止所有的query以及对应的知识库查询结果，是以分级的方式保存在memory中的。
  • copy机制增强的decoder：
    从词汇表中生成词，或者从知识库multi-level memory中复制词，或者从对话历史(context)中复制词。
Fig.1. 模型的整体框架图
来源:Revanth Reddy2019

分级encoder

在第t轮，对话历史共有2t-1个句子$\lbrace{c_1,c_2,…,c_{2t-1}}\rbrace$，其中用户对话为t轮，回复对话为t-1轮。 每个句子$c_i$都是词序列$\lbrace{w_{i1},w_{i2},…,w_{im}}\rbrace$。
每个句子$c_i$先经过embedding layer得到词向量表示，再经过单层bi-GRU得到句子的向量表示$\varphi(c_i)$。$h_{ij}^e$表示词$w_{ij}$对应的隐藏状态。
再将$\varphi{c_i}$经过另一个单词GRU来得到context的向量表示$c$。

multi-level memory

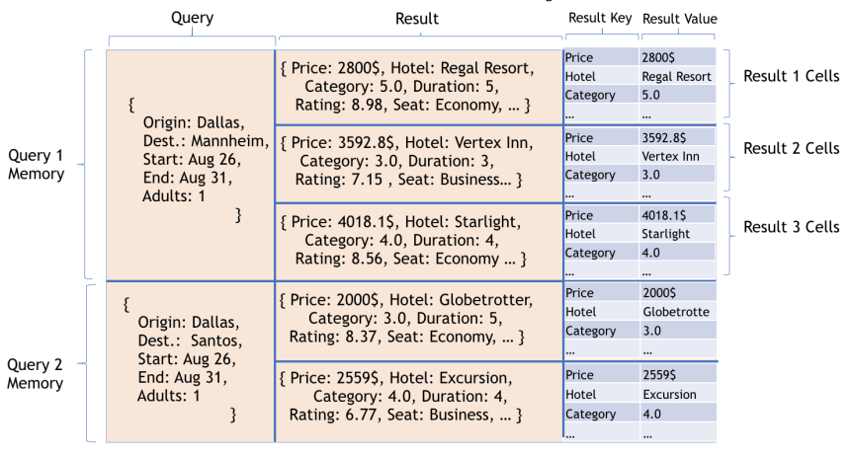
memory的关键是分级的分为三级：query $\to$ result $\to$ result key和result value。见Fig.2。
记本轮对话之前所有的知识库query为$q_1,…,q_k$。每个query $q_i$是一个(key,value)对，$q_i = \lbrace{k_a^{q_i}:v_a^{q_i},0< a< n_{q_i}}\rbrace $。其中key和value分别对应query的槽(slots)和槽值，$n_{q_i}$是query $q_i$的槽值个数。
第j轮对话，用query $q_i$查询知识库的返回结果为result $r_{ij}$。$r_{ij}$也是一个key-value对，$r_{ij} = \lbrace{k_a^{r_{ij}}:v_a^{r_{ij}},0< a < n_{r_{ij}}}\rbrace$。其中$n_{r_{ij}}$是key-value对的个数。

Fig.2. multi memory
来源:Revanth Reddy2019
第一级memory是query的向量表示。 $q_i$的向量表示为$q_i^v$，$q_i^v$为所有values $v_a^{q_i}$的词袋(bag of words)向量表示。 第二级memory是result的向量表示。同样地，$r_{ij}$的向量表示为$r_{ij}^v$，$r_{ij}^v$为所有values $v_a^{r_{ij}}$的词袋(BOW)向量表示。 第三级memory是result的key-value对，$(k_a^{r_{ij}}:v_a^{r_{ij}})$，其中value $v_a^{r_{ij}}$可能会被复制到回复中。

copy机制增强的decoder

decoder一个词一个词地生成回复。在时间步t生成词$y_t$时，可能从词汇表中生成，也能从两个分开的memory上复制。用门$g_1$来选择是从词汇表上生成，还是从memory中复制。如果是后者，用另一个门$g_2$来选择是从context中复制，还是从知识库复制。

  1. 从词汇表生成词
    时间步t，decoder的隐藏状态$h_t$为$$h_t = GRU(y_{t-1},s_{t-1})$$用$h_t$计算在encoder的所有隐藏状态上的attention权重，采用”concat attention”机制：$$a_{ij} = softmax(w_1^\top tanh(W_2tanh(W_3[h_t,h_{ij}^e]))) = \frac{w_1^\top tanh(W_2tanh(W_3[h_t,h_{ij}^e]))}{\sum_{ij}w_1^\top tanh(W_2tanh(W_3[h_t,h_{ij}^e]))}$$则context vector为$$d_t = \sum_{ij}a_{ij}h^e_{ij}$$ $h_t$和$d_t$连接后经过线性层和softmax层得到在词汇表上的概率分布：$$P_g(y_t) = softmax(W_1[h_t,d_t] + b_1)$$
  2. 从context memory中复制词
    直接将计算context vector时的attention权重，作为在context所有词$w_{ij}$上的概率分布：$$P_{con}(y_t = w) = \sum_{ij:w_{ij}=w}a_{ij}$$
  3. 从KB memory中复制实体
    时间步t的隐藏状态$h_t$和context vector $d_t$用来计算在所有query上的attention权重。第一级在所有query $q_1,q_2,…,q_k$的attention权重为$$\alpha_i = softmax(w_2^\top tanh(W_4[h_t,d_t,q_i^v])) = \frac{w_2^\top tanh(W_4[h_t,d_t,q_i^v])}{\sum_{i}w_2^\top tanh(W_4[h_t,d_t,q_i^v])}$$
    第二级$\beta_i$在$q_i$对应的$r_i$上的attention权重为$$\beta_{ij} = softmax(w_3^\top tanh(W_5[h_t,d_t,r_{ij}^v])) = \frac{w_3^\top tanh(W_5[h_t,d_t,r_{ij}^v])}{\sum_{j}w_3^\top tanh(W_5[h_t,d_t,r_{ij}^v])}$$
    第一级attention和第二级attention的乘积是在所有result上的attention权重分布。则memory总的向量表示为$$m_t = \sum_{i}\sum_j\alpha_i\beta_{ij}r_{ij}^v$$
    第三级memory为result的key-value对$(k_a^{r_{ij}}:v_a^{r_{ij}})$，类似于(Eric and Manning, 2017)，用key $k_a^{r_{ij}}$来计算attention权重，将对应的value $v_a^{r_{ij}}$复制到回复中。在$r_{ij}$所有keys上的attention权重为$$\gamma_{ijl} = softmax(w_4^\top tanh(W_6[h_t,d_t,m_t,k_l^{r_{ij}}]))$$则在所有values $v_a^{r_{ij}}$的概率分布为:$$P_{kb}(y_t = w) = \sum_{ijl:v_l^{r_{ij}}=w}\alpha_i\beta_{ij}\gamma_{ijl}$$
  4. decoding
    我们用门机制$g_2$来来结合$P_{con}(y_t)$和$P_{kb}(y_t)$，得到memory上的copy概率分布$P_c(y_t)$。$$g_2 = sigmoid(W_7[h_t,d_t,m_t]+b_2)$$ $$P_c(y_t) = g_2P_{kb}(y_t) + (1-g_2)P_{con}(y_t)$$ 用门机制$g_1$来结合$P_{c}(y_t)$和$P_{g}(y_t)$来得到总的概率分布$P(y_t)$：$$g_1 = sigmoid(W_8[h_t,d_t,m_t]+b_3)$$ $$P(y_t) = g_1P_g(y_t) + (1-g_1)P_c(y_t)$$

相似论文