【来源】:ACL2019
【链接】:https://arxiv.org/abs/1906.02448
【代码、数据集】: 无
这篇论文由中科院发表,获得了ACL2019的 “best long paper”。
要解决的问题
在Neural Machine Translation(NMT)任务中,模型通常采用encoder-decoder框架,基于RNN 或 CNN 或attention。假设输入为$X = \lbrace{x_1,x_2,…,x_m}\rbrace$,真实输出为$Y = \lbrace{y_1^*,y_2^*,…,y_n^*}\rbrace$,预测输出为$Y’ = \lbrace {y_1’,y_2’,…,y_m’}\rbrace$。
第一个问题是:decoder会一个词一个词地生成整个回复。在train阶段,在时间步t生成$y_t’$时,decoder会根据之前真实的词$\lbrace{y_1^*,y_2^*,…,y_{t-1}^*}\rbrace$来预测$y_t’$。在infer阶段,由于不可能知道真实输出,在时间步生成$y_t’$时,decoder会根据之前预测的词$\lbrace{y_1’,y_2’,…,y_{t-1}’}\rbrace$来预测$y_t’$。
可以看到train阶段与infer阶段所依据的词是不同的,train阶段和infer阶段预测的词$y_t’$来自两个不同的概率分布,分别是数据分布(data distribution)和模型的分布(model distribution),这种差别称为“爆炸偏差(exposure bias)”。随着预测序列的长度增加,错误会逐渐累积。
为了解决第一个问题,消除train阶段和infer阶段的这种差别,一个可能的解决方法是:在train阶段,decoder同时根据真实的词$\lbrace{y_1^*,y_2^*,…,y_{t-1}^*}\rbrace$和预测的词$\lbrace{y_1’,y_2’,…,y_{t-1}’}\rbrace$来生成$y_t’$。
第二个问题是: NMT模型通常最优化$Y与Y’$之间的交叉熵目标函数来更新模型参数,但交叉熵函数会严格匹配预测输出$Y’$与真实的输出$Y$。但在NMT任务中,一句话可以有多个不同但合理的翻译。一旦预测输出$Y’$的某个词与$Y$不同,尽管它是合理的,也会被交叉熵函数纠正。这种情况称为“过度纠正的现象”。
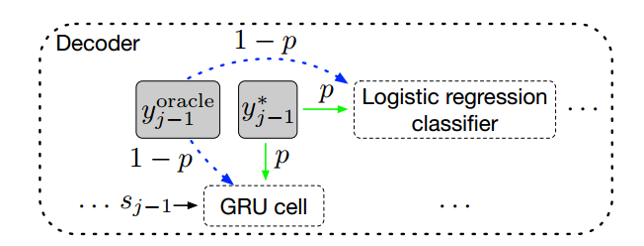
为了消除train阶段与infer阶段的差别,论文提出了一种在train阶段做改进的解决方案。首先,从预测的词中选择oracle word $y_{j-1}^{oracle}$,设真实输出中上一个词为$y_{j-1}^{*}$。接着从$\lbrace{y_{j-1}^{oracle},y_{j-1}^{*}}\rbrace$中抽样一个词,抽中$y_{j-1}^{*}$的概率为$p$,抽中$y_{j-1}^{oracle}$的概率为$1-p$。最后,decoder根据抽样的这个词来预测$y_j$。
在train阶段刚开始时,抽中真实的词$y_{j-1}^{*}$的概率比较大,随着模型逐渐收敛,抽中预测的词$y_{j-1}^{oracle}$的概率变大,让模型有能力处理”过度纠正的问题”。
RNN-based NMT Model
NMT任务常采用encoder-decoder框架,可以基于RNN或CNN或纯attention。论文提出的消除train阶段和infer阶段差别的方法,可以用于任何NMT模型。论文以基于RNN的NMT模型为例,来介绍这种方法。这一节先介绍RNN-based NMT模型。下一节介绍NMT模型如何结合这种方法。
encoder
记输入为$X = \lbrace{x_1,x_2,…,x_m}\rbrace$,真实输出为$Y = \lbrace{y_1,y_2,…,y_n}\rbrace$。encoder采用bi-GRU分别获取正向和反向的隐藏状态$\overrightarrow{h_i},\overleftarrow{h_i}$。$x_i$的embedding向量为$e_{x_i}$。$$\overrightarrow{h_i} = GRU(e_{x_i},h_{i-1})$$ $$\overleftarrow{h_i} = GRU(e_{x_i},h_{i+1})$$ 将$\overrightarrow{h_i},\overleftarrow{h_i}$连接起来,作为$x_i$对应的隐藏状态:$$h_i = [\overrightarrow{h_i},\overleftarrow{h_i}] \tag{1}$$
attention
attention机制用来联系encoder和decoder,更好地捕捉source sequence的信息。也就是在时间步t,通过encoder所有的隐藏状态$\lbrace h_1,h_2,…,h_m \rbrace$来计算context vector $c_t$。记decoder上一时间步的隐藏状态为$s_{t-1}$。 $c_t$是encoder所有隐藏状态$\lbrace h_1,h_2,…,h_m \rbrace$的加权和:$$c_t = \sum_{i=1}^{m}\alpha_{ti}h_i \tag{2}$$ 其中$\alpha_{ti}$是attention权重,计算方式为:$$\beta_{ti} = v_a^\top tanh(W_as_{t-1} + U_ah_i) \tag{3}$$ $$\alpha_{ti} = softmax(\beta_{ti}) = \frac{exp(\beta_{ti})}{\sum_jexp(\beta_{tj})}$$
decoder
decoder采用单向GRU的变体,隐藏状态更新公式为:$$s_t = GRU(s_{t-1},e_{y_{t-1}^*},c_t) \tag{4}$$ 最后根据e_{y_{t-1}^*},decoder的隐藏状态$s_t$,对应的context vector $c_t$来预测$y_t$。 $$o_t = W_og(e_{y_{t-1}^*},s_t,c_t) \tag{5}$$ 在词汇表上的概率分布为:$$P_t(y_t = w) = softmax(o_t) \tag{6}$$
方法
为了消除或减轻train阶段和infer阶段的差别,论文提出 从真实的词$y_{t-1}*$和$y_{t-1}^{oracle}$预测的词中抽样,decoder根据抽样的词来预测下一个词$y_t$。使用论文提出的方法,在时间步t预测$y_t$分为三步:
- 先从预测的词中选择$y_{t-1}^{oracle}$。 论文提出了两种方法来选择oracle word,分别是词级别的方法和句子级别的方法。
- 从$\lbrace{y_{t-1}^{oracle},y_{t-1}*}\rbrace$中抽样得到$y_{t-1}$,抽中$y_{t-1}*$的概率为$p$,抽中$y_{t-1}^{oracle}$的概率为$1-p$。
- 用抽样的词$y_{t-1}$来替换公式$(4)(5)$中的$y_{t-1}^*$来预测下一个词。
oracle word的选择
传统的方法中,decoder会根据上一个时间步真实的$y_{t-1}^*$来预测$y_t$。为了消除train阶段的infer阶段的差别,可以从预测的词中选择oracle word $y_{t-1}^{oracle}$来代替$y_{t-1}^*$。一种方法是每个时间步采用词级别的greedy search来生成oracle word,称为word-level oracle(WO),另一种方法是采用beam-search,扩大搜索空间,用句子级的衡量指标(如:BLEU)对beam-search的结果进行排序,称为sentence-level oracle(SO).
word-level oracle
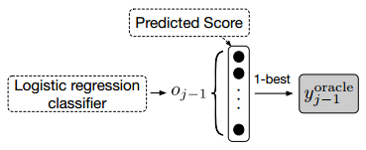
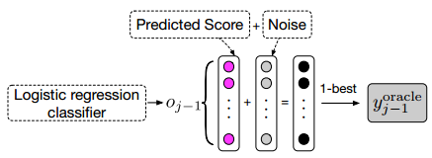
选择$y_{t-1}^{oracle}$最简单直观的方法是,在时间步t-1,选择公式$P_{t-1}$中概率最高的词作为$y_{t-1}^{oracle}$,如Fig.2所示。 为了获得更健壮的$y_{t-1}^{oracle}$,更好地选择是使用gumbel max技术来冲离散分布中进行抽样,如Fig.3所示。
具体地讲,将gumbel noise $\eta$作为正则化项加到公式(5)中的$o_{t-1}$,再进行softmax操作得到$y_{t-1}$的概率分布。$$\eta = -log(-log(u)) $$ $$\tilde{o_{t-1}} = \frac{o_{t-1} + \eta}{\tau} \tag{7}$$ $$\tilde{P_{t-1}} = softmax(\tilde{o_{t-1}}) \tag{8}$$ 其中变量$u \sim U(0,1)$服从均匀分布。$\tau$为温度系数,当$\tau \to 0$时,公式(8)的softmax()逐渐相当于argmax()函数;当$\tau \to \infty$时,softmax()函数逐渐相当于均匀分布。
则$y_{t-1}^{oracle}$为$$y_{t-1}^{oracle} = y_{t-1}^{WO} =argmax(\tilde{P_{t-1}}) \tag{9}$$需要注意的是gumbel noise $\eta$只用来选择oracle word,而不会影响train阶段的目标函数。
sentence-level oracle
为了选择sentence-level oracle word,首先要进行beam-search解码,设beam size为k,得到k个candidate句子。在beam-search解码的过程中,生成每个词时也应用gumbel max技术。
接着,得到k个candidate句子后,用句子级衡量指标BLEU来给这k个句子打分,得分最高的句子为oracle sentence $Y^S = \lbrace{y_1^S,y_2^S,..,y_{|y^S|}^S}\rbrace$。
则时间步t解码对应的oracle word $y_{t-1}^{oracle}$为$$y_{t-1}^{oracle} = y_{t-1}^{SO} = y_{t-1}^{S} \tag{10}$$ 当模型从真实输出$Y$和sentence oracle $Y^S$抽样,这有一个前提是,这两个序列的长度需要是一致的。但beam-search decode不能保证解码序列的长度。为了保证这两个序列长度一致,论文提出了force decoding的解决方法。
force decoding
设真实输出$Y = \lbrace{y_1,y_2,…,y_n}\rbrace$的序列长度为n。force decoding需要解码得到长度同样为n的序列,以特殊字符”EOS”结束。设beam search decode时,时间步t对应的概率分布为$P_t$。
- 当$t< n$时,对于概率分布$P_t$,即使字符”EOS”是概率最高的词,那么生成概率次高的词。
- 当$t = n+1$时,对于概率分布$P_{n+1}$,即使字符”EOS”不是概率最高的词,也要生成”EOS”。
果真是强制生成长度为n的序列。这样beam-search decode得到的序列与真实输出序列的长度就是一致的,都为n。
递减抽样
根据公式(9)或(10)得到$y_{t-1}^{oracle}$后,下一步是从$\lbrace{y_{t-1}^{oracel},y_{t-1}^*}\rbrace$中抽样,抽中$y_{t-1}^*$的概率是p,抽中$y_{t-1}^{oracle}$的概率是1-p。在训练的初始阶段,如果过多地选择$y_{t-1}^{oracle}$,会导致模型收敛速度慢;在训练的后期阶段,如果过多地选择$y_{t-1}^*$,会导致模型在train阶段没有学习到如何处理infer阶段的差别。
因此,好的选择是:在训练的初始阶段,更大概率地选择$y_{t-1}^*$来加快模型收敛,当模型逐渐收敛后,以更大概率选择$y_{t-1}^{oracle}$,来让模型学习到如何处理infer阶段的差别。从数学表示上,概率$p$先大后逐渐衰减,$p$随着训练轮数$e$的增大而逐渐变小。$$p = \frac{\mu}{\mu + exp(\frac{e}{\mu})} \tag{11}$$其中,$\mu$是超参数。$p$是轮数$e$的单调递减函数。$e$从0开始,此时,$p=1$。
训练
将采样得到的$y_{t-1}$代替公式(4)-(6)中的$y_{t-1}^*$来预测$y_t$在词汇表上的概率分布。采用最大似然估计,相当于最小化以下目标函数:$$L(\theta) = -\sum_{n=1}^{N}\sum_{j=1}^{|y_n|}logP_j^n[y_j^n]$$
