【来源】:ICLR2017
【链接】:https://arxiv.org/abs/1611.01603
【代码、数据集】: https://github.com/allenai/bi-att-flow
这是由华盛顿大学和艾伦人工智能研究所发表的论文。艾伦人工智能研究所是大名鼎鼎的微软联合创始人保罗·艾伦创建的。
这是一篇经典的论文,截至目前被引次数高达678次。论文最大的贡献是在阅读理解任务中提出了双向attention机制(BiDirectional attention flow, BiDAF),BiDAF也可以用在其他任务中。
阅读理解任务定义
给定文章context $\lbrace{x_1,x_2,…,x_T}\rbrace$及query $\lbrace{q_1,q_2,…,q_J}\rbrace$,在文章context中找到某个段span作为query的答案。输出其实是这个span的起始坐标和结束坐标。
模型结构
设encoder包含embedding层和Bi-LSTM层,经过encoder后的context representation为$H = \lbrace{h_1,h_2,…,h_T}\rbrace$,query representation为$U = \lbrace{u_1,u_2,…,u_J}\rbrace$。其中$H \in R^{2d\times T}, U \in R^{2d\times J}$。
传统attention机制的几个特征
先介绍传统attention的计算方式。在时间步t计算传统attention时,需要用到上个时间步t-1的decoder RNN的隐藏状态$s_{t-1}$。decoder RNN的隐藏状态更新公式为:$$s_t = f(s_{t-1},y_{t-1},c_t)$$其中c_t为context vector,计算方式为:$$c_t = \sum_{i=1}^{T}\alpha_{t,i}h_i$$ $$\alpha_{t,i} = softmax(\beta_{t,i})$$ $$\beta_{t,i} = score(s_{t-1},h_t)$$其中score(s,h)函数计算s与t之间的相似度。
从传统attention的计算方式可以看出,传统attention有以下几个特征:
- attention权重用来将所有的context representation $\lbrace{h_1,h_2,…,h_T}\rbrace$总结为一个固定维度的向量$c_t$。这个过程不可避免地会带来信息丢失。
- 时间步t的attention权重$\alpha_{t_i}$计算 依赖于上一个时间步的向量$s_{t-1}$。这里可以看出,attention权重的计算是有记忆的。
- attention的计算是单向的。
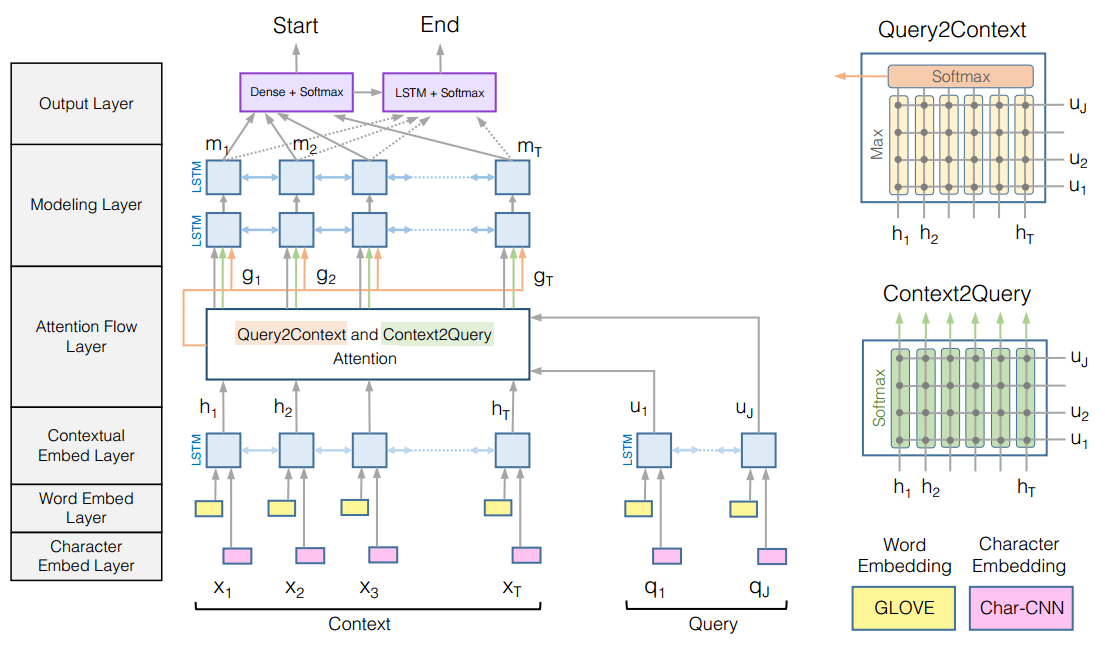
双向attention机制
论文中模型分为了6层,这里只介绍最关键的一层:attention flow layer。该层的输入是context representation $H$和query representation $U$,输出是意识到query的context words representation $G$,以及前一层的context representation。
- 相似度矩阵S
先定义一个 $H\in R^{2d\times T}$和 $U\in R^{2d\times J}$之间的共享相似度矩阵$S\in R^{T\times J}$。其中$S_{tj}$衡量了第t个context word与第j个query word之间的相似度。$$S_{tj} = \alpha(H_{:t},U_{:j}) \in R$$ 其中$H_{:t}\in R^{2d}$是H的第t个列向量,$U_{:j}\in R^{2d}$是U的第j个列向量。$\alpha()$是一个计算相似度的函数:$$\alpha(h,u) = w_{(S)}[h;u;h·u]$$ - context-to-query attention
表示对于每个context word,哪个query word是最相关的。
对于第t个context word,在所有query words $\{q_1,q_2,…,q_J\}$上的attention权重为$a_t\in R^{J}$,有$$\sum_{j}a_{tj} = 1$$
attention权重$a_t$的计算方式为:$$a_t = softmax(S_{t:}) \in R^{J}$$ 对于第t个context word的attended query vector为$$\widetilde{U_{:t}} = \sum_{j}a_{tj}U_{:j} \in R^{2d}$$ 对于所有的context words $\{x_1,x_2,…,x_T\}$,则有$\widetilde{U} \in R^{2d\times T}$ - query-to-context attention
表示对于每个query words,哪个context word是最相似的,对于回答query最重要。
计算在所有context words ${x_1,…,x_T}$上的attention权重为 $$b = softmax(max_{col}(S)) \in R^{T}$$其中$max_{col}(S) \in R^{T}$函数表示在矩阵$S \in R^{T\times J}$的列上取最大值。
则attended context vector为$$\widetilde{h} = \sum_{t}b_{t}H_{:t} \in R^{2d}$$ 这个向量的含义是对于query所有重要的context words的加权和。
把$\widetilde{h}$在列上复制T次,得到了$\widetilde{H} \in R^{2d\times T}$ - 输出融合
把上一层的context representation $H$和attended vector $\widetilde{H}$和$\widetilde{U}$总结组合起来得到意识到query的context words representation $G$,计算方式为:$$G_{:t} = \beta(H_{:t},\widetilde{U_{:t}},\widetilde{H_{:t}}) \in R^{d_{G}}$$ 其中$\beta()$函数可以是任意神经网络,比如MLP多层感知机。论文中采用了简单的连接操作,将$\beta()$函数定义为:$$\beta(h,\widetilde{h},\widetilde{u}) = [h;\widetilde{u};h \circ \widetilde{u};h \circ \widetilde{h}] \in R^{8d\times T}$$
从双向attention机制的计算可以看出,双向attention机制有以下几个特征:
- 与传统attention将所有context representation $\lbrace{h_1,h_2,…,h_T}\rbrace$总结为一个固定维度的向量$c_t$不同。双向attention机制为每个时间步都计算attention,并将attended vector $\widetilde{H}$、$\widetilde{U}$和前一层的context representation $H$流动到下一层。这样减少了提前总结为固定维度的向量带来的信息损失。
- 这是无记忆的attention机制。当前时间步的attention计算只取决于当前的context representation $H$和query representation $U$,而不依赖于上一个时间步的attention。 这种无记忆的attention机制将attention layer和model layer分隔开,迫使attention layer专注于学习context与query之间的attention,而model layer专注于学习attention layer输出内部之间的联系。
- 双向attention机制是双向的,包含query-to-context attention和context-to-query attention,可以彼此之间相互补充。
