【链接】:https://arxiv.org/abs/1908.10731
【代码、数据集】:无
论文的研究内容是conditional text generation,基于knowledge facts的单轮对话。基于给定的对话历史和外部知识,生成合适的回复。论文中将K句话的个人描述作为knowledge facts。
论文采用的模型是seq2seq模型 + attention机制 + 分级pointer network。
论文的亮点是对比模型的思路,可以重点学习一下如何设计对比模型。
任务定义
输入分为两部分:对话历史$X = (x_1,…,x_n)$和K个相关的knowledge facts,其中第i个knowledge fact为$f^i = (f^i_1,…,f^i_{n_i}),i\in \lbrack 1,K \rbrack$。要求生成输出$Y = (y_1,…,y_m)$。
模型
baseline: seq2seq模型 + attention机制
seq2seq模型是基于encoder-decoder框架的。encoder包括embedding层和LSTM层,对于输入$X$,经过encoder得到相应的向量表示 $\lbrace{h_1,…,h_n}\rbrace$。decoder采用单向LSTM,设时间步t的隐藏状态为$s_t$,隐藏状态更新公式为:$$s_t = f(s_{t-1},y_t,c_t)$$ 其中$s_{t-1}$是上一个时间步decoder的隐藏状态,$y_{t-1}$是上一个时间步的输出。c_t为用attention机制计算得到的context vector。计算过程如下:$$c_t = \sum_{i=1}^{n}\alpha_ih_i$$ $$\alpha_i = softmax(\beta_i)$$ $$\beta_i = score(s_{t-1},h_i)$$ 其中$score(s,h)$是计算$s$和$h$之间相似度的函数。
在时间步t,decoder的隐藏状态$s_t$和对应的context vector $c_t$,经过线性层和softmax层,得到在固定词汇表上的概率分布。$$p_g(y_t) = softmax(W[h_t,c_t] + b)$$
可以看出“seq2seq模型 + attention机制”可以用来完成”text-to-text”的text generation的任务。输入是text,没有其他的附加信息(比如knowledge,persona,context等),输出也是text。根据输入的不同,可以得到以下三个模型。
- SEQ2SEQ + NOFACT
只把对话历史$X$作为encoder的输入。 - SEQ2SEQ + BESTFACTCONTEXT
- 先从K个knowledge facts $\lbrace{f^1,…,f^K}\rbrace$中选择与dialog context $X$最相似的fact $f^c$
- 再将$f^c$与dialog context $X$连接起来的$[X;f^c]$,作为encoder的输入。
- SEQ2SEQ + BESTFACTCONTEXT
- 先从K个knowledge facts $\lbrace{f^1,…,f^K}\rbrace$中选择与truth response $Y$最相似的fact $f^r$
- 再将$f^r$与dialog context $X$连接起来的$[X;f^r]$,作为encoder的输入。
从这三个对比试验,可以表明是否添加knowledge fact,以及knowledge fact的不同的选择,对回复生成的影响。
Memory Network
“seq2seq模型 + attention机制”容易遇到 generic response的问题,需要添加附加信息作为额外的输入,来得到信息更丰富的回复。与直接把knowledge fact $f$与dialog context $X$的连接$[X;f]$作为encoder的输入不同,用Memory Network可以更好地结合knowledge facts这样的附加信息。
Memory Network的作用是可以更有效地结合knowledge facts,persona description,dialog context这样的附加信息。Memory Network的工作原理可以分成两个部分:Memory representation 和 read Memory。
- Memory representation
实质上是对附加信息通过另一个facts encoder的向量化表示。$\lbrace{f^1,…,f^K}\rbrace$通过另外一个encoder来编码,经过线性变换分别得到key vectors $\lbrace{k_1,…,k_K}\rbrace$和value vectors$\lbrace{m_1,m_2,…,m_K}\rbrace$。 - read Memory
实质上是计算在$\lbrace{f^1,…,f^K}\rbrace$的attention。论文中用context encoder的最后一个隐藏状态$u$作为query,计算得到总的memory representation: $$o = \sum_{i=1}^K\alpha_im_i$$ $$\alpha_i = softmax(\beta_i)$$ $$\beta_i = score(u,k^i)$$ 最后把context encoder的最后一个隐藏状态$u$和总的memory representation $o$组合起来,$$\hat{u} = u + o$$ 接着用$\hat{u}$来初始化decoder的隐藏状态。
根据是否使用attention机制,可以得到以下四个模型:
- MEMNET
用Memory Network来结合附加信息knowledge facts,用$\hat{u}$来初始化decoder的隐藏状态。
实际上相当于没有用attention机制的seq2seq模型。 - MEMNET + CONTEXTATTENTION
用Memory Network来结合附加信息knowledge facts,用$\hat{u}$来初始化decoder的隐藏状态。
另外在decoder的每个时间步,用decoder的隐藏状态$s_{t-1}$作为query,计算在context encoder的输出context representation $\lbrace{h_1,…,h_n}\rbrace$上的attention,得到总的context vector $c_t^{(c)}$。$$c_t^{(c)} = \sum_{i=1}^{n}\alpha_ih_i$$ $$\alpha_i = softmax(\beta_i)$$ $$\beta_i = score(s_{t-1},h_i)$$ 将$c_t^{(c)}$作为decoder隐藏状态更新的输入:$$s_t = f(s_{t-1},y_{t-1},c_t^{(c)})$$ - MEMNET + FACTATTENTION
用Memory Network来结合附加信息knowledge facts,用$\hat{u}$来初始化decoder的隐藏状态。
另外在decoder的每个时间步,用decoder的隐藏状态$s_{t-1}$作为query,计算在facts encoder的输出facts representation $\lbrace{m_1,…,m_K}\rbrace$上的attention,得到总的facts vector $c_t^{(f)}$。 $$c_t^{(f)} = \sum_{i=1}^K\alpha_im_i$$ $$\alpha_i = softmax(\beta_i)$$ $$\beta_i = score(s_{t-1},k_i)$$ 将$c_t^{(f)}$作为decoder隐藏状态更新的输入:$$s_t = f(s_{t-1},y_{t-1},c_t^{(f)})$$ - MEMNET + FULLATTENTION
同时在context representation $\lbrace{h_1,…,h_n}\rbrace$和facts representation $\lbrace{m_1,…,m_K}\rbrace$上用attention,得到context vector $c_t^{(c)}$和facts vector $c_t^{(f)}$。把二者连接起来,作为decoder隐藏状态更新的输入。$$s_t = f(s_{t-1},y_{t-1},[c_t^{(c)},c_t^{(f)}])$$
seq2seq模型 + copy机制
seq2seq模型只能从固定的词汇表中生成word。Pointer Network的作用是可以从source input中来复制word。用Pointer Network来实现copy机制也可以分为两个部分。
- 计算在所有input tokens $\lbrace{x_1,…,x_n}\rbrace$上的attention权重分布,作为在 $\lbrace{x_1,…,x_n}\rbrace$上的概率分布。
- 使用一个“soft switch”机制,在copy模式时,从source input $\lbrace{x_1,…,x_n}\rbrace$中复制word;当在generation模式时,从固定的词汇表中生成word。
单纯的“seq2seq模型 + attention机制”,再结合copy机制可以得到以下三种模型:
- SEQ2SEQ + NOFACT + COPY
- SEQ2SEQ + BESTFACTCONTEXT + COPY
- SEQ2SEQ + BESTFACTRESPONSE + COPY
分级Pointer Network
单纯的Pointer Network可以从单句话中复制word,使用分级Pointer Network可以从K句话中复制word。
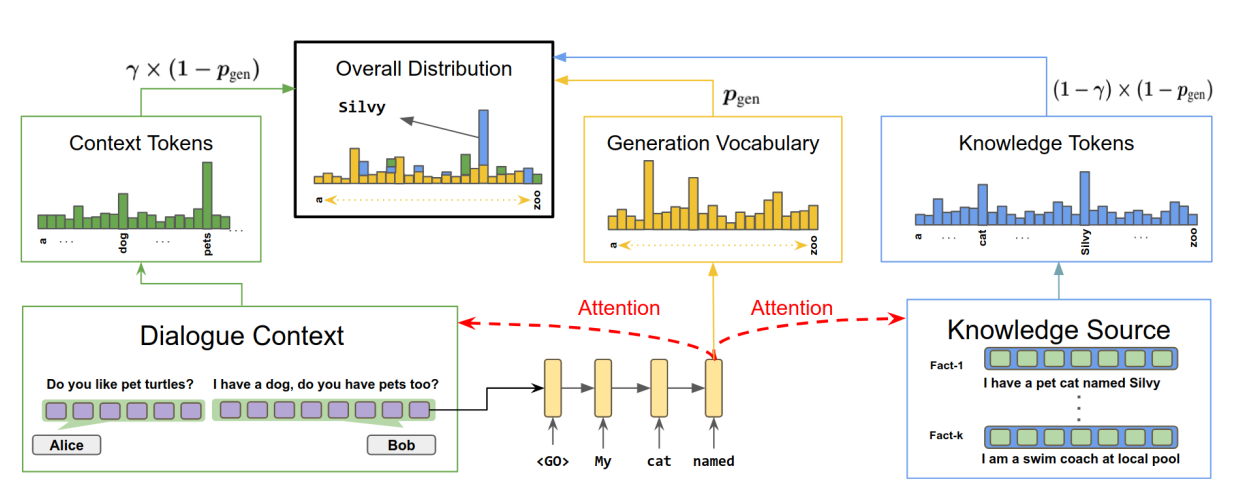
从dialog context中复制word
dialog context $X = \lbrace{x_1,…,x_n}\rbrace$经过context encoder后的context representation为$\lbrace{h_1,…,h_n}\rbrace$,设时间步t,decoder的上一个隐藏状态为$s_{t-1}$。用attention机制:$$c_t^{(x)} = \sum_{i=1}^n\alpha_i^{c}h_i$$ $$\alpha_i^{(x)} = softmax(\beta_i^{(x)})$$ $$\beta_i^{(x)} = score(s_{t-1},h_i)$$ 则从dialog context $X = \lbrace{x_1,…,x_n}\rbrace$中复制word的概率分布为$$p_{copy}^{(x)}(y_t) = \alpha_i^{(x)} i \in [1,n]$$
从knowledge facts中复制word
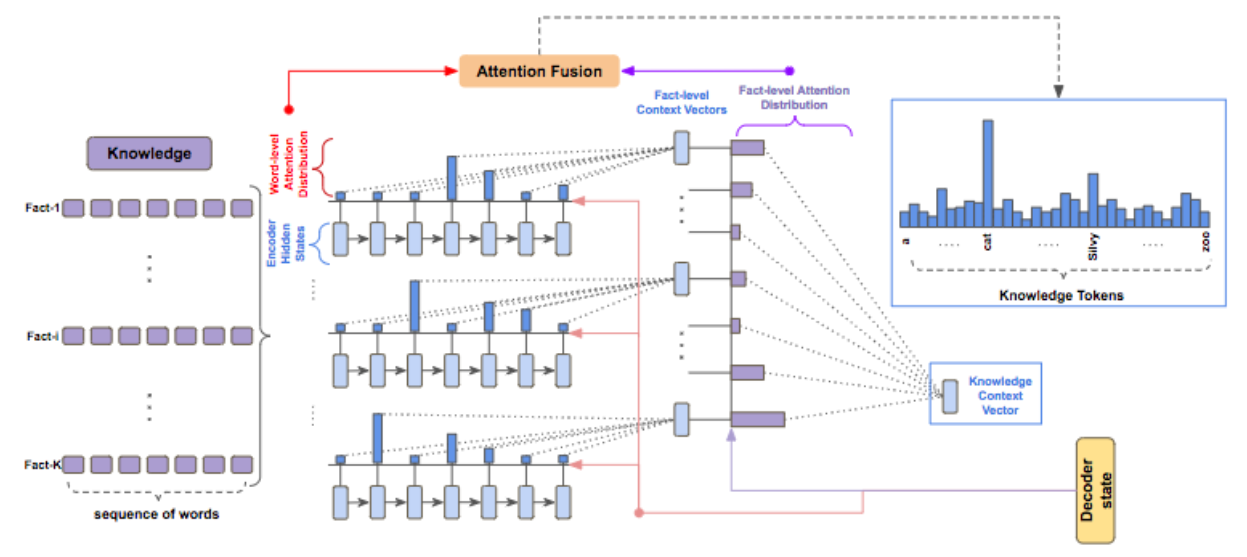
knowledge facts包含K个句子$\lbrace{f^1,…,f^K}\rbrace$,其中$f^i = \lbrace{f^i_1,…,f^i_{n_i}}\rbrace$。经过facts encoder后,再经过线性转换,得到词级别的keys vector和values vector分别为$\lbrace{k_1^{f^i},…,k_{n_i}^{f^i}}\rbrace$和$\lbrace{m_1^{f^i},…,m_{n_i}^{f^i}}\rbrace$。设时间步t,decoder的上一个隐藏状态为$s_{t-1}$。用词级别的attention机制:$$c_t^{f^i} = \sum_{j=1}^{n_i}\alpha_j^{f^i}m_j^{f^i} i\in \lbrack {1,K}\rbrack $$ $$\alpha_j^{f^i} = softmax(score(s_{t-1},k_j^{f^i})) i\in [1,K],j\in [1,n_i]$$ 其中$c_t^{f^i}, i\in [1,K]$是K个句子$\lbrace{f^1,…,f^K}\rbrace$句子级别的向量表示。使用句子级别的attention机制:$$c_t^{(f)} = \sum_{i=1}^{K} = \beta_i^fc_t^{f^i}$$ $$\beta_i^f = softmax(score(s_{t-1},c_t^{f^i})) i\in [1,K]$$ 其中从$c_t^{(f)}$是knowledge facts总的向量表示。
则从knowledge facts中复制word的概率分布为:$$p_{copy}^{(f)}(y_t) = \beta_i^f\alpha_j^{f^i} i\in [1,K],j\in [1,n_i]$$
总的复制word的概率分布
为了把复制word的两个概率分布$p_{copy}^{(x)}$和$p_{copy}^{(f)}$结合起来,使用decoder的隐藏状态$s_t$在context representation $c_t^{(x)}$和总的facts representation $c_t^{(f)}$上用attention机制。得到attention权重分布为$\lbrack{\gamma,1- \gamma}\rbrack$。$$c_t = \gamma c_t^{(x)} + (1 - \gamma) c_t^{(f)}$$ $$\lbrack{\gamma,1-\gamma}\rbrack = softmax(\lbrack{score(s_{t-1},c_t^{(x)}),score(s_{t-1},c_t^{(f)})\rbrack})$$其中$c_t$既包含了dialog context的信息,也包含了knowledge facts的信息,可以用来更新decoder的隐藏状态。$$s_t = f(s_{t-1},y_{t-1},c_t)$$ 则总的复制word的概率分布为$$p_{copy}(y_t) = \gamma \cdot p_{copy}^{(x)} + (1 - \gamma) \cdot p_{copy}^{(f)}$$
soft switch
soft switch可以把copy模式和generation这两种模式结合起来。用一个门机制$p_{gen}$来控制是从固定的词汇表中生成词,或者从dialog context和knowledge facts中复制词。$$p_{gen} = sigmoid(W\lbrack{s_t,c_t}\rbrack)$$ $$p(y_t) = p_{gen} \cdot p_g(y_t) + (1 - p_{gen}) \cdot p_{copy}(y_t)$$
损失函数
采用负对数似然函数作为优化的目标函数,对于单个word的loss函数为:$$loss(\Theta) = -log(p(y_t|y_{<t},X,\lbrace{f^i}\rbrace_{i=1}^K))$$其中$\Theta$表示模型所有的可训练参数,$y_{<t}$表示$y_t$之前所有的word。则对于一个训练样本的loss函数为:$$J_{loss}(\Theta) = -\frac{1}{|Y|}\sum_{t=1}^{|Y|}log(p(y_t|y_{<t},X,\lbrace{f^i}\rbrace_{i=1}^K))$$
