【链接】:https://arxiv.org/abs/1901.09672
【代码、数据集】:无
三星电子中国、清华大学黄明烈教授提交到ARXIV的论文。论文的研究内容是基于persona的单轮对话系统。
数据集描述
论文中构建了一个PersonaDialog的数据集,但数据集没有公开。数据是从微博上爬取,把用户的博文作为对话的post,把用户的评论作为回复。persona是用键值对来描述用户的属性(年龄、性别、地址、兴趣标签等)。而不是用几句话的文本来描述用户画像的。
任务定义
给定单句的对话历史$X = \lbrace{x_1,…,x_n\rbrace}$,以及回复者的N个属性$T = \lbrace{t_1,…,t_N\rbrace}$,其中$t_i = <k_i,v_i>$为键值对。要求生成与用户的画像相一致的回复$Y = \lbrace{y_1,y_2,…,y_m\rbrace}$。$$Y^* = \underset{Y}{arg max} P(Y|X,T)$$
模型结构
基本框架当然是seq2seq模型+attention机制。将对话历史$X = \lbrace{x_1,…,x_n}\rbrace$经过encoder编码为$\lbrace{h_1,…,h_n}\rbrace$。设时间步t,decoder的上一个隐藏状态为$s_{t-1}$,计算attention得到总的context vector $c_t$:$$c_t = \sum_{i=1}^n\alpha_ih_i$$ $$alpha_i = softmax(\beta_i)$$ $$\beta_i = score(s_{t-1},h_i) = V^T\cdot tanh(W^1_{\alpha}s_{t-1} + W^2_{\alpha}h_i) \tag{1}$$decoder RNN的隐藏状态更新公式是:$$s_t = f(s_{t-1},y_{t-1},c_t)$$ 生成$y_t$的概率分布为:$$p(y_t) = softmax(W_os_t + b_{out})$$
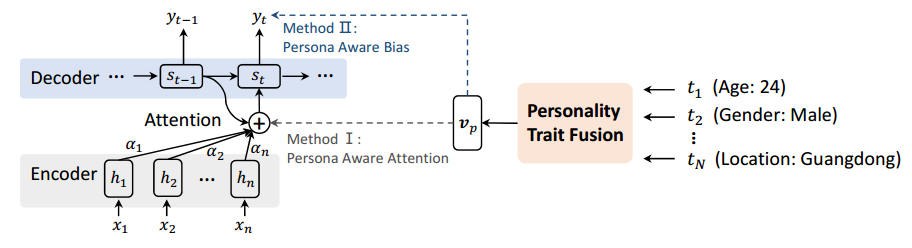
Personality Trait Fusion
这个模块用来把整合persona得到persona representation $v_p$,并用$v_p$来影响decode过程。
将回复者的属性描述$T = \lbrace{t_1,…,t_N}\rbrace$经过embedding层,得到对应的向量表示$\lbrace{v_{t_1},…,v_{t_N}}\rbrace$。论文提出了三种整合persona Trait的方法。
Trait Attention
计算decoder的隐藏状态$s_{t-1}$在Trait representation $\lbrace{v_{t_1},…,v_{t_N}}\rbrace$上的attention,来整合persona Trait,得到persona representation $v_p$。$$v_p = \sum_{i=1}^N\alpha_i^pv_{t_i}$$ $$\alpha_i^p = softmax(\beta_i^p)$$ $$\beta_i^p = score(s_{t-1},v_{t_i}) = V_p^T \cdot tanh(W_p^1s_{t-1} + W_p^2v_{t_i})$$
Trait Average
直接在Trait representation $\lbrace{v_{t_1},…,v_{t_N}}\rbrace$上取平均值,来作为persona representation $v_p$:$$v_p = \frac{1}{N}\sum_{i=1}^Nv_{t_i}$$
Trait Concatenation
直接把Trait representation $\lbrace{v_{t_1},…,v_{t_N}}\rbrace$做连接操作,作为persona representation $v_p$。
使用persona representation $v_p$进行decode
Persona-Aware Attention
让persona representation $v_p$来影响式(1)中attention权重的计算。这种方法可以获得基于persona representation $v_p$的context vector $c_t$。$$\beta_i = f(s_{t-1},h_i,v_p) = V^T \cdot tanh(W^1_{\alpha}s_{t-1} + W^2_{\alpha}h_i + W^3_{\alpha}v_p)$$
Persona-Aware Bias
在输出层结合$v_p$,来影响decode过程。$$p(y_t) = softmax(a_t\cdot W_o^1s_t + (1-s_t)\cdot W_o^2v_p + b_{out})$$ $$a_t = \sigma(V_o^T\cdot s_t)$$ 其中$a_t\in [0,1]$作为一个门机制,来控制生成persona相关的词,或者语义相关的词。
