【来源】：ACL2019
【链接】：https://arxiv.org/abs/1907.10371
【代码、数据集】：https://github.com/Walleclipse/AGPC

北京大学发表在ACL2019的论文。论文的研究内容是基于User profile的评论生成。

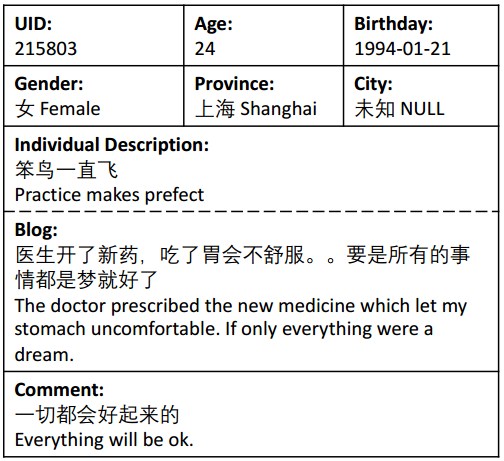
数据集描述

论文从微博收集了一个中文数据集，没有公开，但给出了部分样例数据。这个数据集可以看作基于persona的单轮对话数据集。将微博的博文看作对话历史，将用户的评论看作回复。用户画像包括两个部分，键值对形式的人口统计特征属性（年龄、性别、地区等）和 句子形式的个人描述（微博签名）。

Fig.1. 数据样例

任务定义

给定博文 $X = \lbrace{x_1,…,x_n}\rbrace$和用户画像 $U = \lbrace{F,D}\rbrace$，其中$F = \lbrace{f_1,…,f_k}\rbrace$是用户的数值化属性特征，$D = \lbrace{d_1,…,d_l}\rbrace$是句子形式的个人描述。要求生成与personal profile一致的回复$Y = \lbrace{y_1,…,y_m}\rbrace$。$$Y^* = \underset{Y}{argmax}(Y|X,U)$$

模型结构

Fig.2.模型结构的示意图

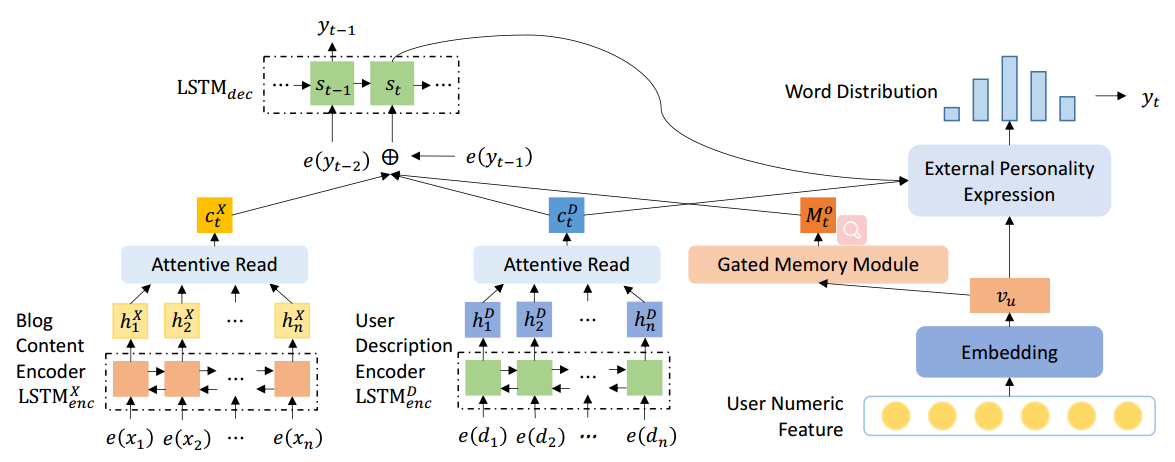
encoder-decoder框架

基本框架当然还是seq2seq模型 + attention机制。$X= \{x_1,…,x_n\}$经过encoder转换为向量表示$h^X = \{h^X_1,…,h_n^X\}$，encoder采用Bi-LSTM。$$h_t^X = LSTM_{enc}^X(h_{t-1}^X,x_t)$$ decoder采用单向LSTM，decoder的隐藏状态更新公式为：$$s_t = LSTM_{dec}(s_{t-1},[c_t^X;e(y_{t-1})]) \tag{1}$$其中$c_t^X$表示时间步t，在所有encoder hidden states $h^X = \{h^X_1,…,h_n^X\}$上使用attention得到的context vector。
则decoder生成词的概率分布为：$$p(y_t) = softmax(W_os_t)$$ 采用负对数似然函数作为目标函数，模型最大化真实回复 $Y^* = \{y_1,…,y_m\}$ 的似然函数：$$Loss = -\sum_{t=1}^m log\Bigl(p(y_t|y_{<t},X,U)\Bigr)$$

User Feature Embedding with Gated Memory

将用户的数值化特征属性$F = \{f_1,…,f_k\}$经过一个全连接层，得到向量表示$v_u$。$v_u$可以看作是user feature embedding，表明用户的个人特征。如果user feature embedding是静态的，在decode过程中会影响生成回复的语法性。为了解决这个问题，设计了一个gated memory来动态地表达用户的个人特征。
在decode过程中，保持一个Internal personal state$M_t$，在decode过程中$M_t$逐渐衰减，decode结束，$M_t$衰减为0，表示用户的个人特征完全表达了。$M_0$的初始值设为$v_u$。 $$g_t^u = sigmoid(W_g^us_t)$$ $$M_0 = v_u$$ $$M_t = g_t^u \cdot M_{t-1},   t>0$$ 引入输出门机制$g_t^o$来充值persona信息的流动：$$g_t^o = sigmoid(W_g^o[s_{t-1};e(y_{t-1});c_t^X])$$ 则时间步t，personal information为：$$M_t^o = g_t^o\cdot M_t$$

Blog-User Co-Attention

实质上是在用户的个人描述$D = \{d_1,…,d_l\}$上使用attention机制。先用另一个persona encoder来编码$D = \{d_1,…,d_l\}$，得到向量表示$\{h_1^D,…,h_l^D\}$。persona encoder采用LSTM: $$h_t^D = LSTM_{enc}^D(h_{t-1}^D,d_t)$$ 在$\{h_1^D,…,h_l^D\}$上使用attention机制，得到总的persona context vector $c_t^D$ $$c_t^D = \sum_{j=1}^k\alpha_{tj}h_j^D$$ $$\alpha_{tj} = softmax(\beta_{tj})$$ $$\beta_{tj} = score(s_{t-1},h_j^D) = s_{t-1}W_ah_j^D$$ 结合$c_t^D$和$c_t^X$作为时间步t总的context vector $c_t$: $$c_t = [c_t^X,c_t^D]$$ 则式（1）中decoder的隐藏状态更新公式变为：$$s_t = LSTM_{dec}(s_{t-1},[c_t;e(y_{t-1});M_t^o])$$

External Personal Expression

通过将internal persona state$M_t$和persona context vector $c_t^D$作为decoder隐藏状态更新的输入，来结合persona信息，进而影响decode过程。这种影响是隐性的，为了更明确地利用用户信息来指导word的生成，将用户信息直接作为输出层的输入。先计算一个user representation $r_t^u$: $$r_t^u = W_r[v_u;c_t^D]$$ 将$r_t^u$作为输出层的输入，则生成词的概率分布为：$$p(y_t) = softmax(W_o[s_t;r_t^u])$$

相似论文

  • 《Personalized Dialogue Generation with Diversified Traits》
    • 笔记链接
    • 异同点比较：
      • 不同点是：本篇论文用internal persona state $M_t$和personal context vector $c_t^D$来作为decoder隐藏状态$s_t$更新的输入，进而影响word的生成。
        而相似的这篇论文中，将personal vector $v_p$ 作为attention机制的query，来attend对话历史。含义是用persona vector $v_p$来选择context相关的信息。
      • 相同点是：两篇论文都把persona information 作为输出层的输入，来明确地影响word的生成。