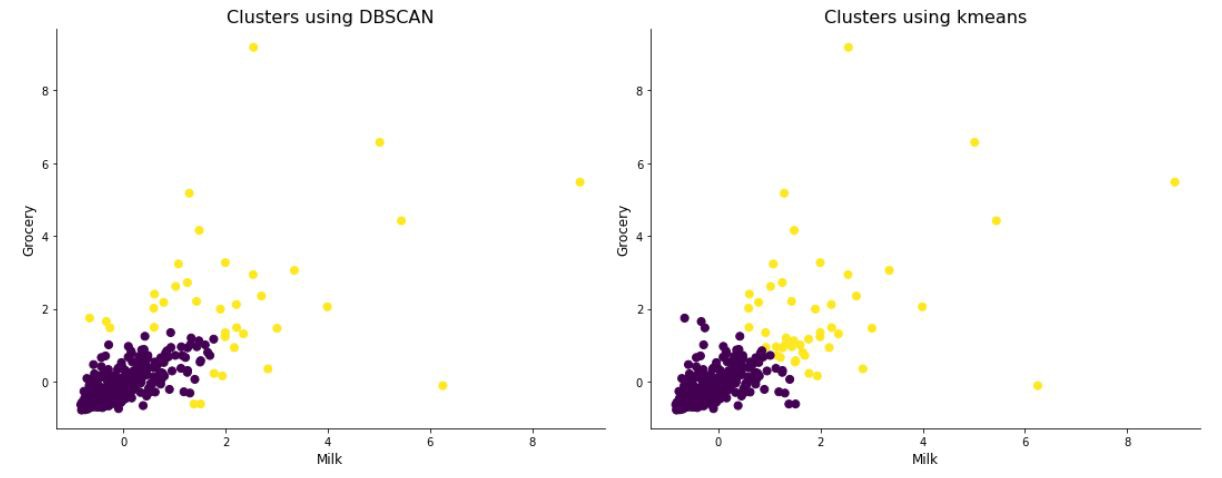
文本聚类就是把一些没有标签的,但有相同特征的数据聚在一起。聚类模型将样本划分为若干个簇(cluster),每个簇对应一些潜在的概念或类别。
K-means算法
K-means聚类是最重要的聚类方法之一。我们假设已经将文档(document)表示为长度归一化的向量表示,也就是将文本数据映射到了欧式空间里。
K-means聚类算法的主要思想是:对于每个簇(cluster),选出一个中心点(cluster center),使得该cluster内的点到该簇中心点的距离小于到其他簇的中心点的距离。我们将簇$w$的cluster center $\vec{\mu}$ 定义为簇的形心: $$\vec{\mu}(w) = \frac{1}{|w|}\sum_{\vec{x} \in w}\vec{x} \tag{1} \label{1}$$ 其中,$|w|$表示簇$w$内 点 的个数。
如何衡量cluster center是否很好地表示了整个cluster内的点呢?我们用cluster内每个点到cluster center的残差平方和(residual sum of squares, RSS)来衡量。对于第$k$个cluster:$$RSS_{k} = \sum_{\vec{x} \in w_{k}}|\vec{x} - \vec{\mu}(w_k)|^{2} \tag{2}$$ 对于整个数据集来说: $$RSS = \sum_{k=1}^{K}RSS_{k} = \sum_{k=1}^{K} \sum_{\vec{x} \in w_{k}} |\vec{x} - \vec{\mu}(w_{k})|^{2} \tag{3} \label{RSS}$$ 上式$\eqref{RSS}$就是K-means聚类算法的目标函数, 我们的目标是最小化该目标函数。
接下来介绍K-means算法的优化迭代过程。第一步是随机选择$K$个点作为cluster center,接下来K-means模型迭代执行两步来最小化目标函数,直到满足停止条件:(1) 固定cluster center $\vec{\mu}(w_k)$,把数据集中的每个点重新分配到最近的cluster center所属的簇中;(2)根据重新分配后簇内的点,重新计算cluster center $\vec{\mu}(w_k)$。我们可以用以下停止条件:
- 固定的迭代次数$maxstep$。限制最大迭代次数 可以限制模型的迭代时间,但有可能由于模型迭代次数不够,导致聚类效果不好。
- 一直迭代到每个cluster内的点不再变化。这样会有很好的聚类效果,但可能导致迭代时间太长。
- 一直迭代到每个cluster的cluster center不再变化。
- 目标函数减小到某个阈值时停止迭代, 这个阈值保证了聚类模型有了不错的聚类效果。
- 目标函数的减少幅度小于某个很小的阈值,这表示聚类模型 接近于收敛了。
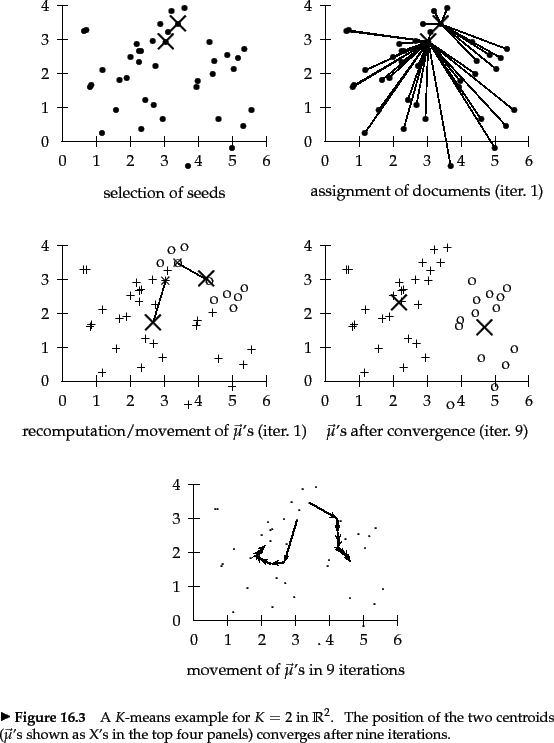
图1展示了K-means聚类算法的伪代码。

目标函数的单调递减性
接下来,我们证明: 每次迭代中,目标函数$RSS$会逐渐减小,从而K-means模型逐渐收敛。
- 在重新分配 点 的过程中,由于把每个点分配到 离它最近的 cluster center对应的簇中,从而目标函数$RSS$是减小的。
- 在重新计算cluster center的过程中,当cluster center为cluster的形心时,$RSS_k$达到它的最小值。证明如下: $$RSS_k(\vec{v}) = \sum_{\vec{x} \in w_k}|\vec{x} - \vec{v}|^2 = $\sum_{\vec{x} \in w_k} \sum_{m=1}^{M}(x_m - v_m)^2 \tag{4} \label{4}$$ 其中$\vec{x}$和$\vec{v}$是一个$M$维的向量,$x_m, v_m$分别是其对应向量的第$m$个值,令该式$\eqref{4}$的偏导数等于0:$$\frac{\partial{RSS_k(\vec{v})}}{\partial{v_m}} = \sum_{\vec{x} \in w_k}2(v_m - x_m) = 0$$ $$v_m = \frac{1}{|w_k|}\sum_{\vec{x} \in w_k}x_m \tag{5} \label{5}$$ 式子$\eqref{5}$是形心公式$\eqref{1}$的逐点表示形式。当偏导数=0时,即$\vec{v} = \vec{\mu{w_k}}$时,式子$\eqref{4}$取得最小值。
需要注意的是,K-means算法不能保证得到目标函数的最小值,这与初始中心点的选择有关。选择不同的初始中心点,可能会得到不同的聚类结果。如果数据集中包含多个离群点(远离其他的点,从而不适合分到任何一个簇中),这样的离群点被选为初始中心点,在迭代过程中不会有其他的任何一个点被分配到这个簇中,迭代结束后我们会得到一个只有一个点的簇(singleton cluster)。即使还有其他的聚类方法,可以得到更小的目标函数值。
因此,初始中心点的选择是个重要的问题。有以下几种方法:
- 把离群点从初始中心点的候选集中排除。
- 选择不同的初始中心点进行多次聚类,选择目标函数值最小的聚类结果。
K-means的时间复杂度
假设数据集有$N$个点,每个点的向量表示的维度为$M$,聚类的簇的个数为$K$。K-means算法的大多数时间花在计算向量之间的距离,每次计算的时间复杂度是$\Theta(M)$。在重新分配点的步骤中,需要进行$KN$次距离计算。每次迭代的时间复杂度为$\Theta(KNM)$。进行$I$次迭代的时间复杂度为$\Theta(IKNM)$。 可以看出: K-means算法的时间复杂度与 迭代次数、 簇的个数、样本数、向量空间的维度线性相关。
参考链接
Louvain社区发现算法
Louvain算法是基于模块度(modularity)的社区发现算法,能够发现层次性的社区结构,其优化目标是最大化整个社区网络的模块度。
模块度(Modularity)
模块度是评估一个社区网络划分好坏的度量方法。模块度的物理意义是:模块度越大,同一个社区内的节点之间联系更加紧密,不同社区之间的节点联系更加松散。对于没有权重的无向图,模块度的取值范围是[-1/2,1]。如果 社区内 边的数量超过随机情况下边的数量,那么模块度是一个正值。
模块度的定义是 社区(group, or cluster, or community)内节点之间的实际连边数 与随机情况下连边数 的差值。如何理解随机情况下的连边数呢?对于一个有$n$个节点(nodes),$m$条边(edges)的网络。其中对于节点$v$有$k_v$条边(我们把节点$v$的边数$k_v$成为节点$v$的度)。接下来我们要在满足网络内的节点数$n$、边数$m$、以及每个节点$v$的边数$k_v$保持不变的情况下,生成一个随机网络。具体地,把每条边分成两半(我们称每半条边为一个 stub),每半条边 与 网络中其他的 任意半条边(stub)连接起来,这样我们就得到了一个完全随机的网络。
考虑两个节点有$k_v$条边的$v$和$k_u$条边的$u$。在$2m$半条边中,一个半条边stub连接到另一个半条边的概率是$\frac{1}{2m-1}$,则有$k_v$条半边的节点$v$和有$k_u$条半边的节点$u$的边数为$$\frac{k_vk_u}{2m-1}\approx\frac{k_vk_u}{2m}$$当$m$很大时,可以取近似值。则两个节点之间的实际 连边数与随机情况下 连边数的差值为:$$A_{ij} - \frac{k_i,k_j}{2m} \tag{6} $$
在$2m$个节点对上求和,可以得到整个网络的模块度$Q$: $$Q = \frac{1}{2m}\sum_{i,j}[A_{ij} - \frac{k_ik_j}{2m}]\delta(c_i,c_j) \tag{7} \label{7}$$
$$ \delta(x,y) =
\begin{cases}
1; when x==y \
0; when x!= y
\end{cases} $$
$A_{ij}$表示节点$i$和节点$j$之间边的权重,当网络是无权图是,所有边的权重可以看作是1;
$k_i = \sum_jA_{ij}$表示节点$i$相连的边的权重之和(度数);
$c_i$表示节点$i$所属的社区;
$m = \frac{1}{2}\sum_{ij}A_{ij}$表示所有边的权重之和(边的数目)。
对式子$\eqref{7}$进行简化,$$Q = \frac{1}{2m}\sum_{ij}[A_{ij} - \frac{k_ik_j}{2m}]\delta(c_i,c_j) $$ $$ = \frac{1}{2m}[\sum_{ij}A_{ij} - \frac{\sum_ik_i\sum_jk_j}{2m}]\delta(c_i,c_j) $$ $$= \frac{1}{2m}\sum_{c}[\sum_{in} - \frac{(\sum_{total})^2}{2m}] \tag{8} \label{8}$$ 其中$\sum_{in}$表示社区$c$内部 边的权重之和(数目,对于无权图),$\sum_{total}$表示所有与社区$c$内的节点相连的边的权重之和(数目,对于无权图)。
对式子$\eqref{8}$进一步简化: $$Q = \sum_{c}[\frac{\sum_{in}}{2m} - (\frac{\sum_{total}}{2m})^2]$$ $$=\sum_{c}[e_c - (a_c)^2]$$ 这样模块度可以理解为 社区内部边的权重和 减去 所有与社区内节点相连的边的权重和的平方。对于无权图,模块度为 社区内部的度数 减去 社区内节点的 总度数的平方。
参考链接
DBSCAN密度聚类算法
DBSCAN(Density-Based Spatial Cluster of Applications with Noise,有噪声的基于密度的聚类方法)是非常典型的基于密度的聚类方法。DBSCAN算法是一种基于样本分布密度的聚类算法,密度聚类算法一般假定可以类别通过样本分布的紧密程度来决定。把紧密相连的点划分到同一个簇。
一些基本概念
设数据集为$D = \lbrace{x_1, x_2, …, x_m\rbrace}$。
- 1个核心思想:基于密度
DBSCAN算法可以找到 数据集中所有 样本紧密分布的区域,并分别将这些紧密的区域作为一个一个的簇。 - 2个算法参数
DBSCAN算法用 $\epsilon$-邻域 的概念来衡量样本分布的紧密程度,也就是样本密度。对于样本点$x_j \in D$,该样本点的$\epsilon$-邻域内包含 与$x_j$距离不大于$\epsilon$的子样本集,即$N_{\epsilon}(x_j) = \lbrace{x_i|distance(x_i,x_j) \leq \epsilon\rbrace}$,这个子样本集中的样本数为$|N_{\epsilon}(x_j)|$。- $\epsilon$-邻域的半径$\epsilon$。
- $MinPoints$ 描述了某一样本半径为$\epsilon$的$\epsilon$-邻域中样本个数的阈值。
- 3种样本点
- 核心对象(core point):对于一个样本点$x_j \in D$,如果其$\epsilon$-邻域中至少包含$MinPoints$个样本点,即$|N_{\epsilon}(x_j)| \geq MinPoints$,则$x_j$是核心对象。
- 边界点(boundary point):对于一个样本点$x_j$,它不是核心对象,但它在某个核心对象的$\epsilon$-邻域内,则$x_j$是边界点。
- 噪声点(noise point): 或称为离群点(outlier point)。对于一个样本点$x_j$,它不是核心对象,也不在任何一个核心对象的$\epsilon$-邻域内,则$x_j$是噪声点。
- 样本点之间的4种关系
- 密度直达(directly reachable):如果样本点$x_i$在核心对象$x_i$的$\epsilon$-邻域内,则称$x_i$由$x_j$密度可达。注意密度直达关系不是对称的,此时不能说$x_j$由$x_i$密度直达。
- 密度可达(reachable):对于$x_i$和$x_j$如果存在一个样本序列$p_1,p_2,…,p_T$,其中$p_1=x_i, p_T=x_j$,且$p_t+1$由$p_t$密度直达,则称$x_i$由$x_j$密度可达。密度可达具有传递性,此样本序列中的传递样本$p_1, p_2, …, p_{T-1}$都是核心对象,只有核心对象才能使得其他样本密度直达。 注意密度可达关系也不满足对称性,这可以由密度直达关系的不对称性得到。
- 密度相连(connectedness):对于样本点$x_i$和$x_j$,如果存在核心对象$x_k$,使得$x_i$和$x_j$均可以由$x_k$密度可达,则称$x_i$与$x_j$密度相连。密度相连关系是满足对称性的。
- 密度不相连:不满足密度相连关系的两个样本点$x_i$和$x_j$,属于两个不同的簇,或者其中存在离群点。
如下图所示,图中$MinPoints$为5,红色的点都是核心对象,因为其$\epsilon$-邻域内至少有5个样本点(包括核心对象本身),圆圈内的黑点都是边界点,圆圈以外的黑点都是噪声点。对于某个红点来说,其对应的圈内的其他点都是密度直达的。途中用绿色箭头连起来的核心对象组成了密度可达的样本序列,这些密度可达的样本序列的$\epsilon$-邻域内所有的样本点都是密度相连的。
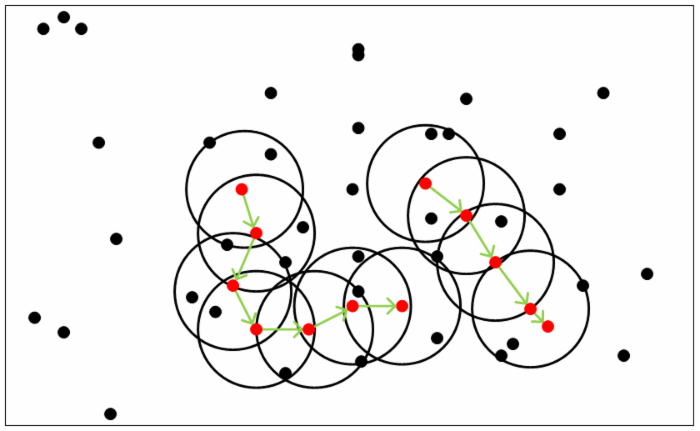
DBSCAN密度聚类思想
DBSCAN的聚类定义为: 把所有密度相连的样本点划分到同一个簇。
DBSCAN密度聚类得到的簇有以下特点:
- 簇内至少有一个核心对象,也就是至少有$MinPoints$个样本点。
- 簇内所有的点都是密度相连的。并且如果某个样本点与某个簇内的其他点密度相连,那么这个样本点属于这个簇。
- 离群点(噪音点)跟所有簇内的点都不是密度相连的,因此,噪音点不属于任何一个簇。
这里需要考虑一个问题,DBSCAN聚类算法会得到有重叠的簇吗?也就是说会有同一个点属于多个簇的情况吗?答案是不会。对于某个样本到两个核心对象的距离都小于$\epsilon$,但这两个核心对象不是密度直达的,不属于同一个簇,怎么界定这个样本点的类别呢?DBSCAN会采取”先来后到”的方式,先进行聚类的类别簇会把这个样本标记为它的类别。 $\tag{9} \label{two}$
DBSCAN聚类算法
输入:样本集$D = \lbrace{x_1, x_2, …, x_m}\rbrace$, 邻域参数($\epsilon, MinPoints$)
输出:簇的划分$C$
- 遍历所有的样本点,找出所有的核心对象。也就是$\epsilon$-邻域内样本数不小于$MinPoints$的样本点。
- 先忽略所有的非核心对象,只考虑核心对象,将所有密度可达的核心对象划分到一个簇。
- 再考虑非核心对象,将每个核心对象$\epsilon$-邻域中的边界点划分到所属的簇中。噪音点不属于任何一个簇。
DBSCAN算法的优缺点
DBSCAN算法有以下优点:
- 与传统的K-means算法相比,DBSCAN算法不需要输入聚类的类别数$K$;
- DBSCAN算法可以发现任意形状的聚类簇。传统的K-means算法一般只适用于 凸样本集的聚类,DBSCAN算法既可以用于凸样本集,也可以用于非凸样本集。
- 对于传统的K-means算法,离群点会影响聚类的结果。DBSCAN算法有噪音点的概念,可以在聚类过程中发现离群点,因此对离群点不敏感。
- 传统的K-means算法,K个随机初始中心点的选择会对聚类结果有很大的影响。相比之下,算法初始值的选择对DBSCAN的聚类结果影响很小(先来后到的例子),DBSCAN的聚类结果是没有偏倚的。
DBSCAN算法的缺点:
- DBSCAN的聚类结果不完全是确定的。对于$\eqref{two}$,聚类结果取决于数据处理的先后顺序。但对于核心对象和噪音点,聚类结果是确定的。对于边界点,聚类结果可能会有所不同。
- 如果数据集的密度不均匀的情况下,DBSCAN的聚类效果比较差。因为当簇之间的密度差别较大时,两个模型参数$\epsilon$和$MinPoints$不可能适合于所有的簇。
- 需要对两个算法参数$\epsilon$和$MinPoints$联合调参,不同的参数组合对聚类效果会有较大影响。