LDA(Latent Dirichlet Allocation, 隐含狄利克雷分布)是一种主题模型，将文档集中每篇文档的主题以概率分布的形式给出。LDA模型是一种词袋(bag-of-words)模型，也就是把一篇文档看作是一组词的集合，而不考虑词与词之间的先后顺序关系。

数学知识

文本建模

日常生活中有大量的文档，文档可以表示为有序的词的序列：$document = \lbrace{w_1, w_2, …, w_n}\rbrace$。

Fig.1 包含m篇文档的语料库 src: LDA数学八卦

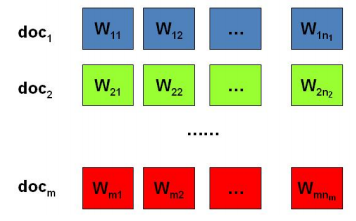
统计文本建模的目的是追问 文档中的词序列是如何生成的。文本可以看作是 上帝抛掷骰子生成的，我们要做的是猜测 上帝是如何抛掷骰子来生成文本的。这里的核心问题有两个：

  1. 上帝有什么样的骰子。
  2. 上帝是如何抛掷这些骰子的。

第一个问题是表示模型中有哪些参数，骰子每一面的概率对应于模型的参数。第二个问题表示了游戏规则是什么，上帝可能有各种不同种类的骰子，按照一定的规则来抛掷这些骰子来生成词序列。
接下来，我们讨论几种猜测如何生成词序列文本的模型。

Unigram Model
文本生成

假设词表中有$V$个词$v_1, v_2, …, v_V$，那么最简单的Unigram Model认为上帝是按照以下的规则来抛掷骰子的。

  1. 上帝只有一个骰子，这个骰子有$V$面，每面对应一个词，每个面的概率是不同的。但每个面的概率是固定的。
  2. 每抛一次骰子，抛出的面对应生成一个词。如果一篇文档有$n$个词，那么依次独立地抛$n$次骰子，就生成了这$n$个词的序列。
Fig.2 上帝抛掷V个面的骰子 src: LDA数学八卦
在这个模型中，模型的参数为各个面的概率$\vec{p} = (p_1, p_2, ..., p_V)$。独立地抛n次$V$个面的骰子，服从多项分布，记作$w \backsim Mult(w|\vec{p})$. 那么生成一篇文档$d = \vec{w} = \lbrace{w_1, w_2, ..., w_n}\rbrace$的概率为 $$p(\vec{w}) = p(w1,w_2,...,w_n) = p(w_1)p(w_2)\cdots p(w_n)$$ 如果语料中有多篇文档$W = \lbrace{\vec{w_1}, \vec{w_2}, ..., \vec{w_m}}\rbrace$，那么语料的概率为: $$p(W) = p(\vec{w_1})p(\vec{w_2})\cdots p(\vec{w_m})$$
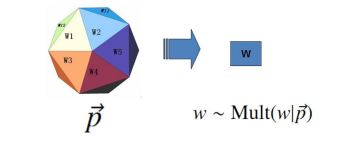
参数估计

参数估计就是估计模型中的参数$\vec{p}$，也就是要估计骰子每一面的概率是多少。采用统计学中 频率派的观点，采用极大似然估计，最大化语料概率$P(W)$，于是参数$p_i$的估计值为$$p_i = \frac{n_i}{N}$$其中$N$是语料中总的词数，$n_i$是词$v_i$在语料中出现的次数。

贝叶斯观点下的Unigram Model
文本生成

对于Unigram Model, 贝叶斯统计学派认为上帝只有唯一一个固定的骰子是不合理的。在贝叶斯学派看来，一切参数都是随机变量，Unigram Model中的骰子$\vec{p}$不是唯一固定的，它也是一个随机变量。按照贝叶斯学派的观点，上帝抛掷骰子的游戏规则，也就是文本生成的过程如下：

  1. 上帝有一个装着无穷多个骰子的坛子，每个骰子有$V$个面。每个骰子各个面的概率是固定的，不同骰子间每个面的概率是不同的。
  2. 上帝先从坛子中抽一个骰子出来，然后用这个骰子抛掷$n$次，就生成了有$n$个词的序列。
Fig.3 Dirichlet先验下的Unigram Model. src: LDA数学八卦
Fig.4 Dirichlet先验下的概率图模型. src: LDA数学八卦
坛子中有无穷多个骰子，骰子$\vec{p}是一个随机变量，$从概率分布的角度来看，骰子$\vec{p}$服从一个概率分布$p(\vec{p})$，这个分布称为参数$\vec{p}$的先验分布。

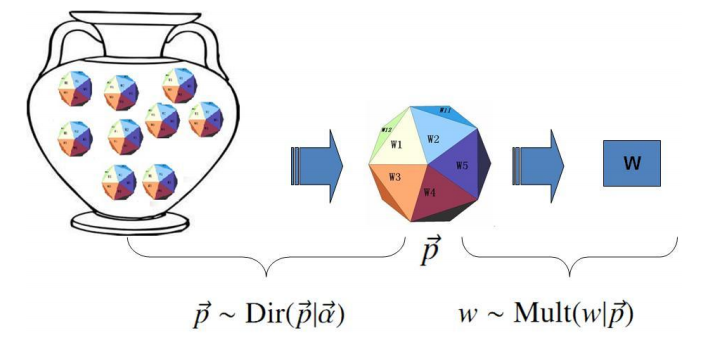
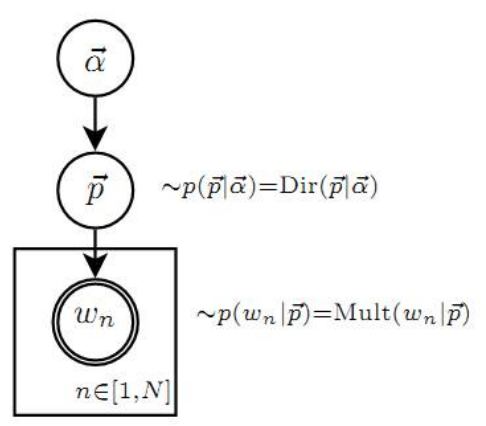
这个先验分布$p(\vec{p})$有很多中选择，我们采用多项分布的共轭分布：Dirichlet分布，有$\vec{p} \backsim Dir(\vec{p}|\vec{\alpha})$,其中$\vec{\alpha} = \lbrace{\alpha_1,\alpha_2, …, \alpha_V}\rbrace$是Dirichlet分布的参数。
多项分布及其共轭分布 Dirichlet分布有以下性质：$$Dirichlet先验分布 + 多项分布的数据 \to 后验分布为Dirichlet分布$$ 加了贝叶斯观点后的区别
原Unigram Model中，只有唯一一个骰子，骰子每个面的概率$\vec{p}$是固定不变的。而贝叶斯观点下，骰子$\vec{p}$不是固定不变的，而应该是一个随机变量，也就是骰子有无穷多个。$\vec{p}$服从一个概率分布，称为$\vec{p}$的先验分布。贝叶斯观点下，多了一个随机变量$\vec{p}$的先验分布。

参数估计

贝叶斯观点下Unigram Model的参数估计可以参见LDA数学八卦。

PLSA主题模型

Unigram Model过于简单。一篇文章通常是由多个主题构成的，比如：一篇nlp相关的文章，可能30%谈论语言学，30%谈论概率统计，20%谈论神经网络，20%谈论计算机。
主题模型中的主题指的是什么呢？一个主题可以用该主题相关的频率最高的一些词来描述。PLSA(Probalilistic Latent Senmantic Analysis)模型认为，一篇文档由多个主题(topics)混合而成，每个topic是在词汇上的概率分布，文章中的每个词都是由一个固定的topic生成的。

文本生成

再回到上帝抛掷骰子上来，PLSA模型认为上帝是按照以下的游戏规则来生成文本的。

  1. 上帝有两个类型的骰子，一类是doc-topic骰子，每个doc-topic骰子有$K$个面，每个面对应一个topic；一类骰子是topic-word骰子，每个topic-word骰子有$V$个面，每个面对应一个词。
  2. 上帝一共有$K$个topic-word骰子，每个topic-word骰子对应一个topic。
  3. 在生成每篇文档前，上帝先为这篇文档制造一个特定的doc-topic骰子。然后重复以下过程生成文档中的词：
    • 抛掷这个doc-topic骰子，得到一个topic；
    • 选择这个topic对应topic-word骰子，抛掷这个topic-word骰子，得到一个词。

PLSA模型文本生成的过程可以图形化地表示为：

Fig.5 PLSA模型的文本生成过程. src: LDA数学八卦
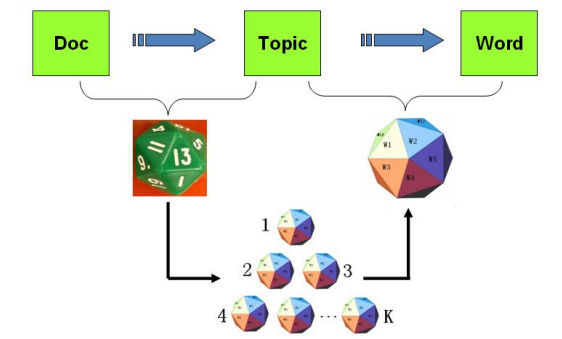
参数估计

PLSA模型有两类参数，也就是doc-topic骰子每个面的概率$p(topic_k|doc_i)$，和$K$个topic-word骰子每个面的概率$p(word_j|topic_k)$。对于包含$M$篇文档的语料$C = ({d_1, d_2, …, d_M})$，每篇文档对应一个特定的doc-topic骰子，所有对应的骰子记为$(\vec{\theta_1}, \vec{\theta_2}, …, \vec{\theta_M})$; 游戏中总共有$K$个topic-word骰子，记为$(\vec{\varphi_1}, \vec{\varphi_2}, …, \vec{\varphi_K})$。

可以使用著名的EM算法来估计PLSA模型的参数。参数估计的求解参见：通俗理解LDA主题模型-CSDN
估计模型参数的过程，实际上就是：根据文档中的词序列来反推其主题分布的过程。doc-topic骰子每个面的概率$p(topic_k|doc_i)$表征了文档的主题分布，topic-word骰子每个面的概率$p(word_j|topic_k)$表征了主题的词分布（PLSA模型认为 topic是在词汇上的概率分布）。

LDA主题模型

对于上述的PLSA模型，doc-topic骰子$\theta_m$和topic-word骰子$\varphi_k$都是模型中的参数，贝叶斯学派认为 参数都是随机变量。类似于Unigram Model的贝叶斯改造，在两个骰子参数前加上先验分布，从而将PLSA的抛骰子游戏过程改造成一个贝叶斯的游戏过程。由于$\varphi_k$和$\theta_m$都对应多项分布，因此先验分布采用Dirichlet分布，于是就得到了LDA(Latent Dirichlet Allocation)模型。总的来说，LDA模型是对PLSA模型的贝叶斯版本。

文本生成

在LDA模型中，上帝是按照以下的规则来玩文档生成的游戏的：

  1. 上帝有两大坛子的骰子，第一个坛子里装了无穷多个doc-topic骰子，第二个坛子里装了无穷多个topic-word骰子。
  2. 上帝随机从第二个坛子里独立地抽取$K$个topic-word骰子，标号$1-K$。
  3. 每次生成一篇文档前，上帝先从第一个坛子里随机抽取一个doc-topic骰子。然后重复以下过程生成文档中的词：
    • 先抛掷这个doc-topic骰子，得到一个topic编号$z$；
    • 从$K$个topic-word骰子中选择编号为$z$的那个，抛掷这个骰子，生成一个词。

PLSA模型与LDA模型的区别

  • PLSA模型中，doc-topic骰子和topic-word骰子是唯一确定的，也就是虽然doc-topic骰子$\vec{\theta_m}$和topic-word骰子$\vec{\varphi_k}$是未知的，但是确定的固定不变的。
  • LDA模型中，doc-topic骰子$\vec{\theta_m}$和topic-word骰子$\vec{\varphi_k}$是未知的，而且是随机变量，不是唯一确定的。这两类随机变量$\vec{\theta_m}$和$\vec{\varphi_k}$服从某个概率分布，我们采用与多项分布的共轭分布：Dirichlet分布。
Fig.6 LDA模型. src: LDA数学八卦

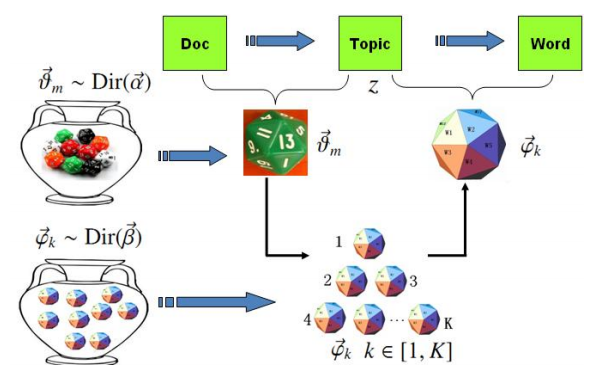
物理过程分解
LDA模型的概率图表示如下图所示：

Fig.7 LDA模型概率图表示. src: LDA数学八卦

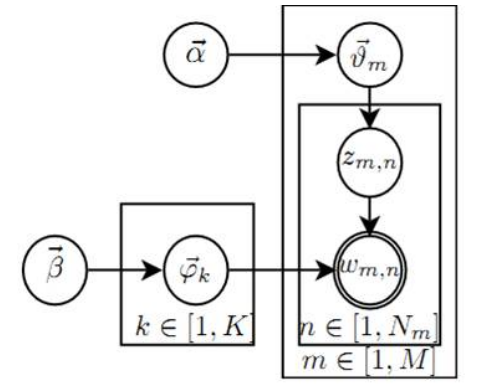
这个概率图可以分解为两个主要的物理过程：

  1. $\vec{\alpha} \to \vec{\theta_m} \to z_{m,n}$: 这个过程表示在生成第$m$篇文档时，先从第一个坛子中抽取一个doc-topic骰子$\vec{\theta_m}$, 再抛掷这个骰子生成文档中的第$n$个词的topic编号$z_{m,n}$。
  2. $\vec{\beta} \to \vec{\varphi_k} \to w_{m,n}|k = z_{m,n}$: 这个过程表示生成第$m$篇文档的第$n$个词时，从第二个坛子中抽取$K$个topic-word骰子$\vec{\varphi} = (\varphi_1, \varphi_2, …, \varphi_K)$，挑选编号为$k = z_{m,n}$的骰子进行抛掷，生成第$n$个词$w_{m,n}$。

换一个角度来解释这两个物理过程：

Fig.8 第一个物理过程. src: LDA数学八卦

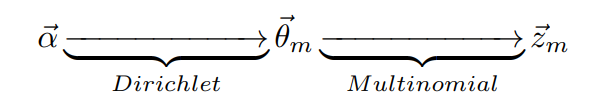
  1. $\vec{\alpha} \to \vec{\theta_m} \to z_{m,n}$表示生成文档中所有词对应的主题。$\vec{\alpha} \to \vec{\theta_m}$对应Dirichlet分布，$\vec{\theta_m} \to z_{m,n}$对应Multinomial分布，整体是一个Dirichlet-Multinomial共轭结构。第一步：从参数为$\vec{\alpha}$的Dirichlet先验分布中采样得到文档的主题分布$\vec{\theta_m}$，这是一个多项式分布；第二步：从参数为$\vec{theta_m}$的多项式分布中采样一个主题$z_{m,n}$。

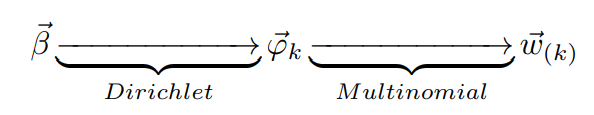    Fig.9 第二个物理过程. src: LDA数学八卦

  2. $\vec{\beta} \to \vec{\varphi_k} \to w_{m,n}|k = z_{m,n}$表示生成文档中的词。$\vec{\beta} \to \vec{\varphi_k}$对应Dirichlet分布，$\vec{\varphi_k} \to w_{m,n}$对应多项式分布，整体是一个Dirichlet-Multinomial共轭结构。第一步：从参数为$\vec{\beta}$的Dirichlet先验分布中采样得到主题的词分布$\vec{\varphi_k}$，这是一个多项式分布；第二步：在这个参数为$\vec{\varphi_k}$的词分布中抽样一个词$w_k$。

参数估计

接下来的问题是，LDA模型怎么由文档来反推每一篇文档的主题分布和每一个主题的词分布呢？一般有两种方法：Gibbs采样算法和变分推断EM算法。详见：LDA数学八卦

参考链接